「必要条件・十分条件の判断が分からない」
「それぞれの意味や見分け方が分からない」
今回は必要条件・十分条件についての悩みを解決します。
 高校生
高校生必要条件とかが本当に分からなくて..
「リンゴならば果物である」のように真偽がはっきりしているものを命題といいます。
命題が正しいとき「真」、反例があるとき「偽」といいます。
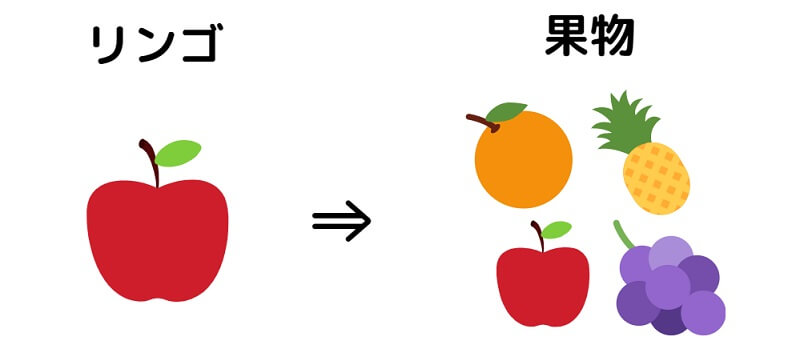
命題「リンゴならば果物である」において、
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”” bgcolor=”#E8F5E9″ borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=””]
- 「リンゴ」は「果物」の十分条件
- 「果物」は「リンゴ」の必要条件
[/st-mybox]
「\(p⇒q\)」という命題が真のとき、
矢印が出ている\(p\)が十分条件、矢印を受けている\(q\)が必要条件です。
このように命題の真偽と矢印の向きで必要条件・十分条件は判断することができます。
本記事では必要条件・十分条件の違いと見分け方を解説します。
本記事を読めば条件の見分け方が分かるようになります。
必要条件・十分条件とは?
まず、必要条件・十分条件の定義を確認しましょう。

 高校生
高校生pとかqで説明されても分からないよ
 シータ
シータそうだよね。
具体的な命題で解説していくよ
真の命題「リンゴならば果物」を例にして考えます。
「リンゴならば果物である」という命題を矢印で表すと「リンゴ⇒果物」です。

[st-mybox title=”ポイント” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#FFFDE7″ borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 矢印が出ているほうが十分条件
- 矢印を受けているほうが必要条件
[/st-mybox]
つまり、リンゴ⇒果物 において
- 「リンゴ」は「果物」の十分条件
- 「果物」は「リンゴ」の必要条件
ここで注意点が1つ
命題が逆になると必要条件・十分条件も逆になります。

つまり、「\(x=1\)」は「\(x+3=4\)」の十分条件でもあり、必要条件でもあります。
このような場合、「\(x=1\)」は「\(x+3=4\)」の必要十分条件といいます。
必要十分条件については後ほど詳しく解説します。
⇒必要十分条件について早く知りたい
 高校生
高校生矢印が出ている方が十分条件なんだね
 シータ
シータそういうこと!
でもそれだけで判断するのは注意だよ
命題の真偽の調べ方
必要条件か十分条件かを判断するには、命題の真偽を判断する必要があります。
命題の真偽と聞くと何だか難しそうですよね。でも、実際はそんなことないです。
ポイントは反例(当てはまらない例)があるかどうかです。
[st-mybox title=”命題の真偽” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
反例がなければ命題は真、反例があればその命題は偽となります。
[/st-mybox]
たとえば、「キリンならば動物です」という命題は真です。なぜならキリンは「植物」でも「食べ物」でもなく動物だからです。

一方で、「動物ならばキリンです」という命題はどうでしょうか。
動物にキリンは含まれますが、「ゾウ」や「ゴリラ」も動物です。
つまり、動物だからといってキリンとは限らないのです。
したがって、反例があるので「動物ならばキリンです」という命題は偽です。
 高校生
高校生当てはまらない例が出せるときは偽になるんだね!
ベン図を使って考える
命題の真偽は条件をベン図で考えるとイメージしやすいです。
\(p\)の集合が\(q\)の集合に含まれるならば、\(p⇒q\)は真です。

ベン図を用いて命題「リンゴならば果物である」の真偽を考えます。
つまり、リンゴが果物という集合に含まれていれば「リンゴ⇒果物」は真となります
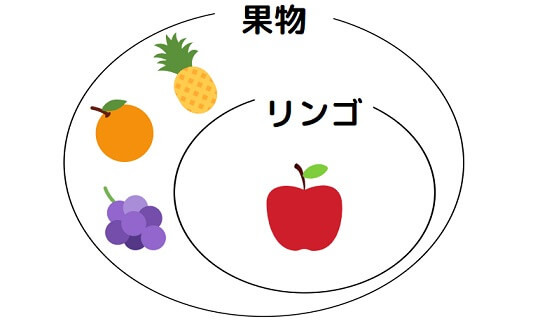
リンゴという集合は果物の集合に含まれます。
つまり、リンゴ⇒果物は真の命題です。
一方で、「果物ならばリンゴである」は偽です。
なぜなら、果物にはブドウやパイナップルも含まれるからです。

「リンゴならば果物である」は真
「果物ならばリンゴである」は偽
必要条件・十分条件の見分け方
必要条件と十分条件の見分け方を解説します。
 高校生
高校生必要条件と十分条件のちがいがよくわかっていなくて…
 シータ
シータここは重要なところだから、じっくり読んで見てね
\(p⇒q\)という命題において、矢印が出ている\(p\)が十分条件です。
一方で、矢印を受けている\(q\)が必要条件となります。
[st-mybox]
命題「リンゴならば果物」において
「リンゴ」は「果物」の十分条件
「果物」は「リンゴ」の必要条件
[/st-mybox]
ベン図を用いて考える場合は、ベン図が広い方が必要条件です。
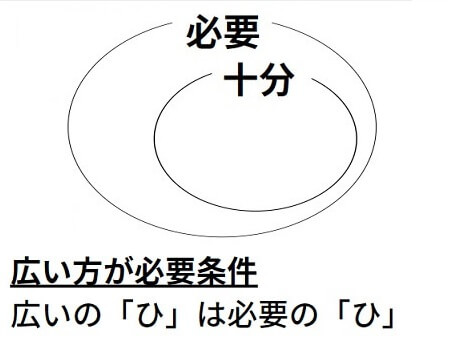
[st-cmemo fontawesome=”fa-lightbulb-o” iconcolor=”#FFA726″ bgcolor=”#FFF3E0″ color=”#000000″ bordercolor=”” borderwidth=”” iconsize=””]広いの「ひ」は必要の「ひ」だと覚えましょう。[/st-cmemo]
十分条件は銃をイメージ
どうしても覚えられない方に向けてとっておきの覚え方を紹介します。
十分条件は「矢印を出しているほう」でした。
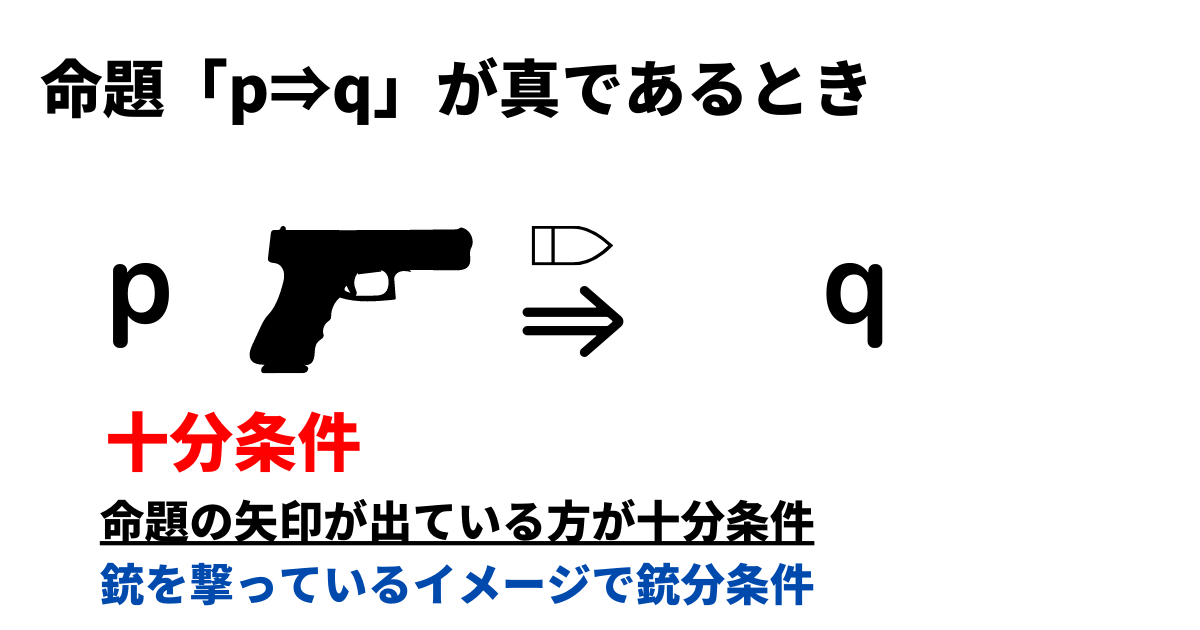
pが銃を撃っているのをイメージして、
矢印を出している=銃を持っている
つまり、十(じゅう)分条件だと覚えましょう。
必要十分条件

\(p⇒q,q⇒p\)がともに真のとき、
\(p\)は\(q\)であるための必要条件であり、十分条件でもあるため必要十分条件といいます。
同様に\(q\)も\(p\)であるための必要十分条件といいます。
こういった場合は「\(p\)と\(q\)は同値」といい、
と表します。
具体的な例を交えて解説します。
以下の2つの条件において,
- \(p:x=1\)
- \(q:x+3=4\)
\(x=1⇒x+3=4\)が成り立つので
「\(x=1\)」は「\(x+3=4\)」の十分条件
また、\(x+3=4⇒x=1\)も成り立つので
「\(x=1\)」は「\(x+3=4\)」の必要条件でもあります。
つまり、「\(x=1\)」は「\(x+3=4\)」の必要十分条件となり以下のように表します。
\(x=1⇔x+3=4\)
 高校生
高校生なんだかわかったような気がする!!
 シータ
シータ最後に例題で確認してみよう
例題で確認してみよう
必要条件・十分条件が理解できているか確かめましょう。
【例題1】
2つの条件「ぶどう」「果物」の関係を考えます。
- \(p:\)ぶどう
- \(q:\)果物
Step1. \(p⇒q\)を考える
まずは「ぶどう ⇒ 果物」を考えます。
ぶどうは果物に含まれるので、これは真の命題です。
Step2. \(q⇒p\)を考える
次に「果物 ⇒ ぶどう」も考えます。
この命題は偽です。
なぜなら果物には「リンゴ」や「バナナ」などの反例が挙げられるからです。
Step3.必要条件・十分条件・必要十分条件を考える
ここでベン図を用いて考えてみると、
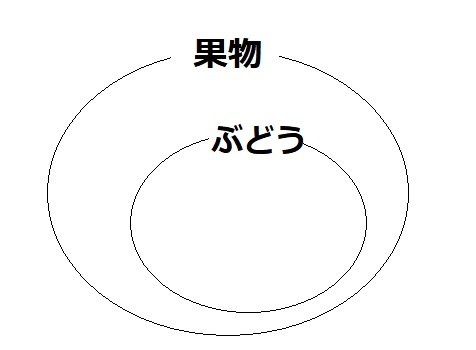
このことからも
- ぶどう ⇒ 果物が真
- 果物 ⇒ ぶどうが偽
であることがわかります。
したがって、「ぶどう⇒果物」が真の命題で
- ぶどうは,果物であるための十分条件
- 果物は,ぶどうであるための必要条件
となります。
【例題2】
次に,\(x^{2}=1\)と\(x=1\)の関係を考えてみます。
- \(p:x^{2}=1\)
- \(q:x=1\)
Step1. \(p⇒q\)を考える
まずは、\(x^{2}=1 ⇒ x=1\)の真偽を調べます。
\(x^{2}=1\)を解くと,\(x=±1\)です。
このとき、\(x=-1\)が反例になるので命題「\(x^{2}=1 ⇒ x=1\)」は偽です。
Step2. \(q⇒p\)を考える
つぎに \(x=1 ⇒ x^{2}=1\)の真偽を調べます。
\(x=1\)のとき,\(x^{2}=1\)だから命題「\(x=1⇒ x^{2}=1\)」は真です。
Step3.必要条件・十分条件・必要十分条件を考える
命題「\(x^{2}=1 ⇒ x=1\)」は偽
命題「\(x=1⇒ x^{2}=1\)」は真
真である命題は「\(x=1⇒ x^{2}=1\)」なので、
\(x^{2}=1\)は,\(x=1\)であるための必要条件
\(x=1\)は,\(x^{2}=1\)であるための十分条件
となります。
【例題3】
最後に以下の条件の関係を考えます。
\(q:x,y\)のうち少なくとも1つは0
Step1. \(p⇒q\)を考える
まず\(p⇒q\)を確かめます。
\(xy=0\)より,\(x=0\)または\(y=0\)
したがって、「\(p⇒q\)」は真です。
Step2. \(q⇒p\)を考える
つぎに\(q⇒p\)を確かめます。
\(x,y\)のうち少なくとも1つが0ならば\(xy=0\)です。
したがって、「\(q⇒p\)」の命題は真です。
Step3.必要条件・十分条件・必要十分条件を考える
命題「\(p⇒q\)」は真
命題「\(q⇒p\)」は真
したがって、
pはqであるための必要十分条件
qはpであるための必要十分条件
つまり、pとqは同値である。
必要条件・十分条件 まとめ
今回は必要条件・十分条件の違いと見分け方を中心に解説しました。

[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”” bgcolor=”#E8EAF6″ borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=””]
2つの条件\(p,q\)において
\(p⇒q\)が真ならば、\(p\)は\(q\)の十分条件
\(q⇒p\)が真ならば、\(p\)は\(q\)の必要条件
\(p⇔q\)が真ならば、\(p\)は\(q\)の必要十分条件
[/st-mybox]

[st-mybox title=”はてな” fontawesome=”fa-question-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 矢印が出ているほうが十分条件
- 矢印を受けているほうが必要条件
[/st-mybox]
命題の真偽を求める方法の1つに対偶の真偽を考える方法があります。
命題の対偶や否定などは「命題の意味と「逆・裏・対偶」の関係」でまとめているので参考にしてください。
[st-card id=”3705″ readmore=”on”]

