「接線ってどうやって求めるの？」
「接線の方程式を求めたい」
今回は2次関数の接線に関する悩みを解決します。
高校生接線ってどうやって求めるんでしたっけ…
さっそくですが、こんな問題見たことありませんか？
練習問題
次の関数の点(0,3)における接線の方程式を求めよう。
\[y=x^2+2x+3\]
こんな問題とか
練習問題
次の関数のグラフに、点(0,0)から引いた接線の方程式を求めよ。
\[y=x^2+3x+4\]
こんな問題です。
「難しそう」と思った方が多いと思います。
しかし、接線の求め方はやり方を覚えたら大したことないです。
本記事では2次関数の接線の求め方を解説します。
この記事を参考にして、接線を求められるようにしましょう。
記事の内容
接線は１次関数
中学校の復習になりますが、直線は１次関数でしたね。
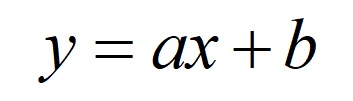
こんな式を覚えていますか？
\(a\)が傾き（変化の割合）で、\(b\)が切片でした。
直線の方程式が求められる条件として、
- 通る点の座標が２つ分かっているとき
- 通る点の座標１つと傾きが分かっているとき
- 通る点の座標１つと切片が分かっているとき
この３つがありました。
どうでしょう、覚えていましたか？
2次方程式の接線は２つ目の条件
「通る点の座標１つと傾きが分かっているとき」
を使って求めることがほとんどです。
やるべきは大きく分けて２ステップ！
１．接線の傾きを求める
２．通る点を代入して完成！
まずは傾きの求め方を伝授していきます。
接線の求め方
接線は2つのステップで求めることができます。
シータやることはたったこれだけ！
step
1接線の傾きを求める
まずは接線の傾きから求めていきましょう。
接線の傾きは、微分して接点の\(x\)座標を代入すると出ます。
例えば、
\(y=x^2+2x+3\)のグラフ上で(0,3)における接線の方程式を求めよ。
この場合、まず\(y=x^2+2x+3\)を\(f(x)\)とでも置きましょう。
\[f(x)=x^2+2x+3\]
この方程式を微分します。
\[f^{\prime}(x)=2x+2\]
次に微分した式に、接点の\(x\)座標を代入します。
接点が(0,3)だったので、\(x=0\)を代入
\[f^{\prime}(0)=2\times{0}+2=2\]
つまり傾きは２となります。
これで接線の傾きを求めることができました。
step
2通る点を代入
接線の傾きの出し方は分かったので、接線の方程式を求めていきます。
接点の座標を代入して引くだけです。
公式としてはこう！
微分可能な関数\(y=f(x)\)上の点\(A(a, f(a))\)における接線の方程式は,\(y-f(a)=f^{\prime}(a)(x-a)\)
\(y=x^2+2x+3\)のグラフ上で(0,3)の接線を考えているので、
\[y-3=f^{\prime}(0)(x-0)\]
これを計算すると、
\[y=2x+3\]
これで接線を求めることができました。
接点が分かっている場合
冒頭に登場したこの問題でも練習していきます。
練習問題
次の関数の点(0,3)における接線の方程式を求めよう。
\[y=x^2+2x+3\]
まずは接線の傾きを出します。
\(f(x)=x^2+2x+3 A(0,3)\)
\(f^{\prime}(x)=2x+2\)
微分した式に、接点の\(x\)座標を代入します。
接点が(0,3)だったので、\(x=0\)を代入
\(f^{\prime}(0)=2\times{0}+2=2\)
傾きが２と分かりました。
傾きは接線の方程式のここに代入します。
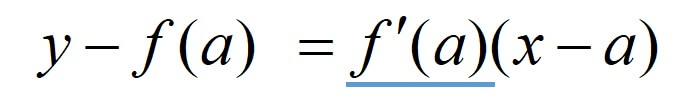
次に接線の座標(0,3)を代入するのですが、ここに代入します。
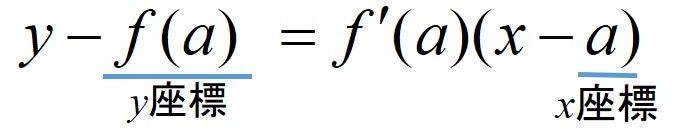
つまり、
\(y-3=2(x-0)\)
となります。
これを式変形して、
\(y=2x+3\)
これが\(y=x^2+2x+3\)上の点\(A(0,3)\)における接線の方程式です。
通る点が分かっている場合
もう１つのパターンもあります。
分かっている座標がグラフ上の点ではなく、接線が通る点のパターンです。
練習問題
次の関数のグラフに、点(0,0)から引いた接線の方程式を求めよ。
\[y=x^2+3x+4\]
これもまず傾きを求めていきます。
\(f(x)=x^2+3x+4\)
\(f^{\prime}(x)=2x+3\)
接点の座標を代入したいのですが問題発生！
与えられている点が接点の座標ではないのです。
ひとまず接点を\((a,a^2+3a+4)\)とでもしましょう。
\(f^{\prime}(a)=2a+3\)
点\((a,a^2+3a+4)\)における接線の傾きが\(2a+3\)だとわかりました。
接線の公式に代入して、
\[y-(a^2+3a+4)=(2a+3)(x-a)\]
分かりずらいけど、これが接線の方程式を表しています。
これが(0,0)を通れば問題と一致するので、x,yにそれぞれ代入して、
\begin{eqnarray}
-a^2-3a-4&=&-2a^2-3a\\
a^2-4&=&0\\
(a+2)(a-2)&=&0\\
a&=&-2,2
\end{eqnarray}
高校生あれ、aの解が2つ出てきました！
疑問に思った方は勘が鋭いですね！
なぜ接点の\(x\)座標を表す\(a\)が２つ出たのかというと、
イメージとしてはこんな感じ！
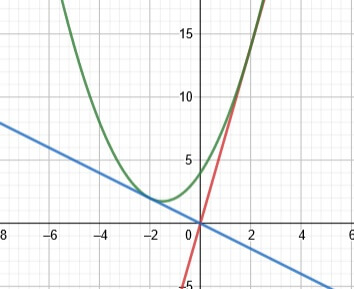
接線が点(0,0)を通る接点が２つあるということですね！
接線の式に\(a\)を代入すると、
\[y-(a^2+3a+4)=(2a+3)(x-a)\]
\(a=-2\)のとき
\begin{eqnarray}
y-2&=&-(x+2)\\
y=-x
\end{eqnarray}
\(a=2\)のとき
\begin{eqnarray}
y-14&=&7(x-2)\\
y=7x
\end{eqnarray}
したがって、\(y=x^2+3x+4\)の接線で、点\((0,0)\)と通る接線の方程式は
\[y=-x\]
\[y=7x\]
2次関数の接線 まとめ
今回は2次関数の接線の求め方をまとめました。
2次関数の接線今回は2次関数に焦点を当てて解説しましたが、3次関数でも接線の求め方は同じです。
シンプルな計算ですが、とても重要な公式なので必ず覚えましょう。
コメント