対数方程式の解き方！真数条件と底の値に注意しよう！

対数の方程式が解けない方は必見！

今回は対数方程式に関するこんな悩みを解決します。

以下のようなlogを含む方程式を対数方程式といいます。

見た目が難しそうなので、解く前から嫌な気持ちが湧いてきますよね。

実は対数方程式の問題は大きく4種類に分かれています。

その解き方さえ理解しておけば、対数方程式のほとんどの問題が解けるようになります。

本記事では対数方程式の解き方と注意点を解説しています。

例題の解説とあわせて、練習問題もあるのでぜひ最後までご覧ください。

※本ページは学習アプリのプロモーションが含まれています。

対数方程式とは？

対数関数を含む以下のような方程式を対数方程式といいます。

この方程式を成り立たせる\(x\)を求めるのが、対数方程式の問題です。

\[log_{3}x+log_{3}(x-1)=12\]

このように方程式が長いと難しく見えますね。

対数方程式の解き方

対数方程式を解くには、以下の形を目指して式変形をしていきます。

つまり、

\(log_{2}x=log_{2}5\)ならば、\(x=5\)というわけです。

とはいえ、こんな簡単な問題はそうそうありません。

そこで、以下の5ステップで対数方程式を解きます。

この5ステップを踏んでいけば、どんな対数方程式でも解くことができます。

このあと4つの例題で解説していきますが、その前に対数方程式を解くときの注意点を知っておきましょう。

真数条件と底の条件に注意

対数方程式を解くときに注意して欲しいことがあります。
それは真数条件と底の条件の確認です。

\(log_{a}b\)における、\(b\)を真数（しんすう）といいます。

真数はどんなときも正の数であり、この条件を真数条件といいます。

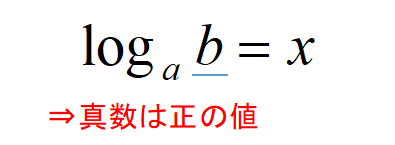
また、底\(a\)にも条件があり、\(a>0,a≠1\)が成り立ちます。

真数条件と底の条件のことを忘れると、正しい方程式の解を求めることができません。

対数方程式や対数不等式を解くときは、まず条件の確認をしておきましょう。

それでは対数方程式の解き方を解説していきましょう。

対数方程式の問題は大きく4つの種類に分けることができます。

基本の問題

まずは対数方程式の基本問題です。

これらの問題は必ず解けるようにしておきましょう。

まず真数条件より、\(x>0 \cdots ①\)

両辺を対数で表します。

\begin{eqnarray}
log_{2}x&=&4\\
log_{2}x&=&log_{2}2^{4}\\
log_{2}x&=&log_{2}16
\end{eqnarray}

両辺の真数を比較して、

\[x=16 \cdots ②\]

①,②より、\(x=16\)

真数条件より、\(x>0\)かつ\(x-2>0\)

したがって、\(x>2 \cdots ①\)

対数法則より、

\begin{eqnarray}
log_{2}x+log_{2}(x-2)&=&3\\
log_{2}x(x-2)&=&log_{2}8
\end{eqnarray}

両辺の真数を比較して、

\begin{eqnarray}
x(x-2)&=&8\\
x^{2}-2x-8&=&0\\
(x-4)(x+2)&=&0
\end{eqnarray}

よって、\(x=-2,4 \cdots ②\)

①,②より、\(x=4\)

底をそろえる問題

両辺の底が異なる方程式もあります。

真数条件より、\(x-3>0\)かつ\(2x-3>0\)

したがって、\(x>3 \cdots ①\)

底の変換公式を使って、底を2でそろえます。

\begin{eqnarray}
log_{2}(x-3)&=&log_{4}(2x-3)\\
\displaystyle log_{2}(x-3)&=&\frac{log_{2}(2x-3)}{log_{2}4}\\
\displaystyle log_{2}(x-3)&=&\frac{log_{2}(2x-3)}{2}\\
\end{eqnarray}

これで両辺の底をそろえることができました。

\begin{eqnarray}
\displaystyle 2log_{2}(x-3)&=&log_{2}(2x-3)\\
(x-3)^{2}&=&2x-3\\
x^{2}-8x+12&=&0\\
(x-2)(x-6)&=&0
\end{eqnarray}

よって、\(x=2,6 \cdots ②\)

①,②より、\(x=6\)

置き換える問題

次は置き換えを使った解き方を解説します。

まず真数条件より、\(x>0 \cdots ①\)

\(log_{2}x=X\)とすると、

\[X^{2}-2X-8=0\]

これを解くと、

\begin{eqnarray}
X^{2}-2X-8&=&0\\
(X-4)(X+2)&=&0\\
X&=&-2,4
\end{eqnarray}

よって、\(log_{2}x=-2,4\)

すなわち、\(\displaystyle x=\frac{1}{4},16 \cdots ②\)

①,②より、\(\displaystyle x=\frac{1}{4},16 \cdots ②\)

底に文字がある問題

底に文字がある場合でも、底の変換公式を使えば問題ありません。

真数条件より、\(x>0 \cdots ①\)

底の条件より、\(x>0,x≠1 \cdot ②\)

\begin{eqnarray}
log_{2}x+3log_{x}2&=&4\\
\displaystyle log_{2}x+3 \cdot \frac{log_{2}2}{log_{2}x}&=&4\\
\displaystyle log_{2}x+\frac{3}{log_{2}x}&=&4\\
\end{eqnarray}

\(log_{2}x=X\)とすると、

\begin{eqnarray}
\displaystyle X-\frac{3}{X}&=&4\\
X^{2}+3&=&4X\\
X^{2}-4X+3&=&0\\
(X-1)(X-3)&=&0
\end{eqnarray}

よって、\(log_{2}x=1,3\)

すなわち、\(x=2,8 \cdots ③\)

①,②,③より、\(x=2,8\)

基礎から丁寧に確認！
プロ講師の分かりやすい解説

ここまで読んで、まだピンと来ていない人いますか？

もしかすると、あなたには文章よりも動画解説のほうが合っているかもしれません。

河合塾が提供する「河合塾One」なら解説が丁寧で、基礎から確認できるのでおすすめです。

しかも、いまなら無料体験で全授業が視聴できます。

⇒いますぐ「12-8：対数関数を含む方程式・不等式」を受講する

対数方程式【練習問題】

対数方程式の練習問題に挑戦してみましょう。

以下が今回の練習問題です。

練習問題1の解説

これは対数法則をつかう基本の問題です。

真数条件より、\(x-2>0\)かつ\(x-3>0\)

すなわち、\(x>3 \cdots ①\)

\begin{eqnarray}
log_{2}(x-2)+log_{2}(x-3)&=&1\\
log_{2}(x-2)(x-3)&=&log_{2}2\\
log_{2}(x^{2}-5x+6)&=&log_{2}2
\end{eqnarray}

真数部分の等式を考えて、

\begin{eqnarray}
x^{2}-5x+6&=&2\\
x^{2}-5x+4&=&0\\
(x-1)(x-4)&=&0
\end{eqnarray}

よって、\(x=1,4 \cdots ②\)

①,②より、\(x=4\)

練習問題2の解説

真数条件より、\(x+2>0\)かつ\(x-3>0\)

よって、\(x>3 \cdots ①\)

\begin{eqnarray}
log_{2}(x+2)&=&log_{4}(x-3)\\
\displaystyle　log_{2}(x+2)&=&\frac{log_{2}(x-3)}{log_{2}4}\\
\displaystyle log_{2}(x+2)&=&\frac{1}{2}log_{2}(x-3)\\
2log_{2}(x+2)&=&log_{2}(x-3)
\end{eqnarray}

対数の性質より、

\[(x+4)^{2}=x+3\]

これを解くと、

\begin{eqnarray}
x^{2}+8x+16=x+3\\
x^{2}+7x+
\end{eqnarray}

練習問題3の解説

真数条件より、\(x>0 \cdots ①\)

\(log_{2}x=X\)とすると、

\begin{eqnarray}
X^{2}-3X-10&=&0\\
(X-5)(x+2)&=&0
\end{eqnarray}

よって、\(X=-2,5\)

すなわち、\(log_{2}x=-2,5\)

したがって、

\[x=\frac{1}{4},32 \cdots ②\]

①,②より、\(x=\frac{1}{4},32\)

対数方程式　まとめ

今回は対数方程式の解き方についてまとめました。

対数方程式　まとめ

どんな対数方程式の問題でも、以下の5ステップで解を求めることができます。

対数方程式の問題は以下の4種類に分けることができる。

対数方程式にはもっと複雑な問題もありますが、今回紹介した4つの解き方を覚えておけば十分です。

ただし、対数方程式を解くにあたって、指数法則や対数法則は必須なので確認しておきましょう。

指数関数・対数関数の総復習がしたい方はこちらの記事はおすすめです。

指数関数・対数関数のまとめ記事へ