「対数ってなに？」
「指数とlogの関係が分からない」
今回は対数に関するこんな悩みを解決します。
高校生logで表すのが苦手です…
対数に苦手意識がある方って多いですよね…
ぼく自身、学生時代は対数が苦手だった覚えがあります。
対数を使うことで、非常にめんどうな計算をスマートに計算することができたりします。
対数
\(a>0,a≠1\)で\(M>0\)において、
\[log_{a}M=x \Leftrightarrow a^{x}=M\]
ただし、真数\(b\)は正の数である。
本記事では対数logの意味と重要な公式について解説します。
この記事を読めば、対数の意味や基本の計算について理解できます。
ここら辺はフワッと理解している方が多いので、しっかり理解して差を付けましょう。
記事の内容
※本ページは学習アプリのプロモーションが含まれています。
シータ気になる見出しをクリックして、
ぜひ最後までご覧ください。
対数とは？logの意味
対数\(log_{a}M\)とは、「\(M\)は\(a\)の何乗なのか」を表したものです。
対数
\(a>0,a≠1\)で\(M>0\)において、
\[log_{a}M=x \Leftrightarrow a^{x}=M\]
ただし、真数\(b\)は正の数である。
\[a^{x}=M\]
\(a\)の\(x\)乗が\(M\)のとき、対数で表すことで
\[log_{a}M=x\]
と表されます。
シータ指数と対数は合わせて理解していこう
対数logの例
2の3乗は8ですよね。
\[2^{3}=8\]
これを対数を使って表すと、
\[log_{2}8=3\]
となります。
\[2^{3}=8 \Leftrightarrow log_{2}8=3\]
これらは指数で表すか、対数で表すかの違いです。
難しく考えすぎないほうが、スムーズに理解できるでしょう。
高校生底aの何乗なのかを表しているんですね
底と真数が表すもの
\(log_{a}b=x\)における\(a\)を底（てい）、\(b\)を真数（しんすう）といいます。
底は指数で表すときにも使う用語なので覚えておきましょう。
指数\(a^{x}=b\)における\(a\)を底、\(x\)を指数といいます。
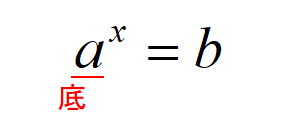
真数条件
対数\(log_{a}b=x\)における真数\(b\)は正の値になります。
この条件のことを真数条件といいます。
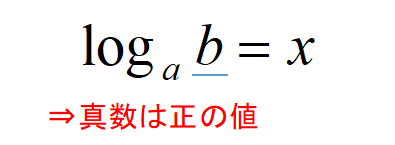
なぜ真数が正の値になるのかは別の記事で解説しています。
高校生真数は必ず正の値なんですね
シータ式変形や証明で出てくるから覚えておこう
対数の重要な公式
対数には重要な公式がいくつかあります。
対数の重要公式
\(a>0,m>0,n>0,a≠1\)において
\(log_{a}a=1\)
\(log_{a}a^{m}=m\)
\(log_{a}b^{m}=m log_{a}b\)
これらは対数の超基本の公式です。
この他にも重要な公式がいくつもあるので、こちらの記事も合わせてご覧ください。
基本公式の例題
対数の基本的な公式をつかった練習問題を解いてみましょう。
例題
次の計算をしてみましょう。
(1) \(log_{3}9\)
(2) \(log_{2}25\)
(1)はすぐに解けるようにしておきましょう。
\begin{eqnarray}
log_{3}9&=&log_{3}3^{2}\\
&=&2
\end{eqnarray}
(2)は最後までlogが残るため少し不安ですが、これで大丈夫です。
\begin{eqnarray}
log_{2}25&=&log_{2}5^{2}\\
&=&2log_{2}5
\end{eqnarray}
シータこの式変形はスムーズにできるようにしよう
高校生問題を解いて特訓しておきます！
指数と対数の関係
ここまで解説したように、指数と対数には密接な関係があります。
以下は指数関数\(y=2^{x}\)のグラフです。
\(x\)の値が大きくなるにつれて、\(y\)が大きくなっていることが分かります。
底a>1の指数関数
- 点\((0,1)\)を通る
- \(x\)が大きくなるほど増加
- \(x\)が小さくなるほど0に近づく
一方で、対数関数\(y=log_{2}x\)は以下のようなグラフになります。
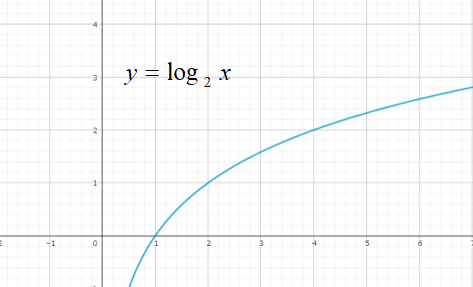
どんな対数関数でも\(log_{a}1=0\)なので、点(1,0)を通過します。
\(y=2^{x}\)と\(y=log_{2}x\)はどちらも底が2の関数です。
底が等しい指数関数と対数関数のグラフを書くと、\(y=x\)に対して対称であることが分かります。
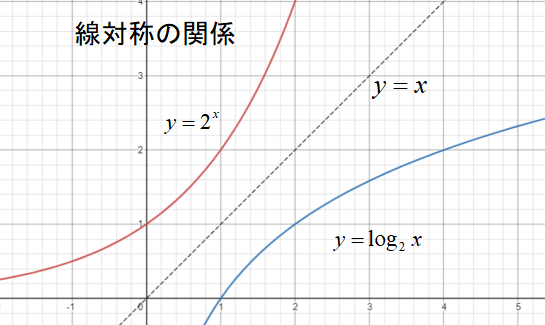
そこまで重要なことではありませんが、知っておいて損はないでしょう。
シータ指数と対数が連動していることが分かるね
指数・対数の練習問題
指数から対数、その逆に対数から指数へ式変形ができるように練習しましょう。
練習問題
指数は対数に、対数は指数に変換してみよう。
(1) \(3^{3}=27\)
(2) \(log_{2}x=8\)
(1) \(3^{3}=27\)から \(log_{3}27=3\)
(2) \(log_{2}256=8\)から \(2^{8}=256\)
高校生いまは分かるけど、また忘れちゃいそうです
シータこれは慣れていくしかないね
対数とは？ まとめ
今回は対数logの意味についてまとめました。
対数log まとめ対数\(log_{a}M\)とは、「\(M\)は\(a\)の何乗なのか」を表したものです。
対数
\(a>0,a≠1\)で\(M>0\)において、
\[log_{a}M=x \Leftrightarrow a^{x}=M\]
ただし、真数\(b\)は正の数である。
真数条件
対数\(log_{a}b=x\)における真数\(b\)は正の値である。
今回は対数の意味について解説してきましたが、対数には多くの公式があります。
対数方程式や対数不等式は解き方を知らないと、手も足も出ないのでぜひ以下の記事もご覧ください。
また、指数関数や対数関数について総復習がしたい方はこちらの記事がおすすめです。
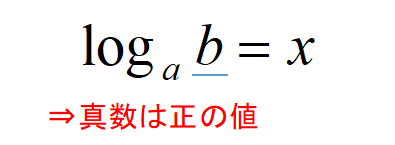
コメント