階差数列を用いた一般項と和を求める公式！初項に階差を足していくだけ

数学B数列において、多くの高校生を悩ませるのが「階差数列」です。

[st-mybox title=”今回解決する悩み” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”4″ borderradius=8″ titleweight=”bold” fontsize=”110″ myclass=”nayami-box” margin=”50px auto 40px”]

「階差数列ってなに？」
「階差数列の一般項の求め方は？」
「和の公式を忘れてしまった」

[/st-mybox]

今回は階差数列に関するこんな悩みを解決します。

階差数列とは「数列\(\{a_{n}\}\)の隣接する項の差を項とする数列」を指します。

階差数列は数列のなかでも、かなり重要な数列の1つです。

階差数列をしっかり理解しておくと、様々な数列の問題に対応できるようになります。

本記事では階差数列を用いた一般項と和の求め方について解説します。

数列が苦手な方や、これから数列を学習する方の参考になるので、ぜひ最後までご覧ください。

[st_af id=”13737″]

階差数列とは？

数列\(\{a_{n}\}\)の隣り合う2つの項の差

\[b_{n}=a_{n+1}-a_{n}　(n=1,2,3,\cdots)\]

を項とする数列\(\{b_{n}\}\)を、数列\(\{a_{n}\}\)の階差数列といいます。

例えば以下のような数列があったとしましょう。

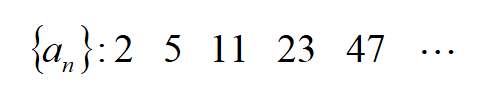
このときの階差数列は初項が3で、3ずつ増加しているので「初項3、公差3の等差数列」となります。

[st-mybox title=”階差数列” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

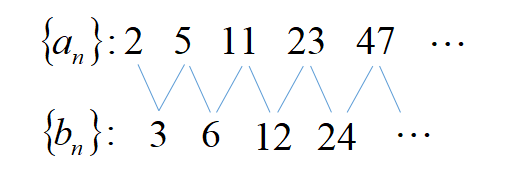
階差数列　⇒　数列\(\{a_{n}\}\)の隣接する項の差を項とする数列

初項：最初の項

等差数列：一定の差で変化する数列

等比数列：一定の比で変化する数列

[/st-mybox]

[st-mybox title=”関連記事” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

等差数列の公式まとめ！一般項と和の公式を分かりやすく解説！

等比数列の公式まとめ！一般項と和の公式を分かりやすく解説！

[/st-mybox]

階差数列と一般項

階差数列を用いた一般項の公式

一般項とは、数列の第\(n\)項\(a_{n}\)を\(n\)や数字を用いて表したものです。

階差数列を用いて、もとの数列の一般項を表すと以下の公式になります。

[st-mybox title=”階差数列と一般項” fontawesome=”” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

数列\(\{a_{n}\}\)の階差数列を\(\{b_{n}\}\)とすると、n≧2のとき

\[a_{n}=a_{1}+\sum_{k=1}^{n-1} b_{k}\]

[/st-mybox]

階差数列を用いた一般項の証明

なぜΣ（シグマ）を使うのでしょうか？

数列の初項\(a_{1}\)に対して、階差数列\(\{b_{n}\}\)を加えていくと考えます。

数列\(a_{1}　a_{2}　a_{3}　a_{4} …　a_{n}\)があります。

この数列の階差数列を\(\{b_{n}\}\)とすると、

[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\(a_{1}=a_{1}\)←初項

\(a_{2}=a_{1} + b_{1}\)

\(a_{3}=a_{1} + b_{1}+b_{2}\)

\(a_{4}=a_{1} + b_{1}+b_{2}+b_{3}\)

[/st-mybox]

このように初項\(a_{1}\)に階差数列の項を加えていくので、

[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\(a_{1}=a_{1}\)

\(a_{2}=a_{1} + b_{1}\)

\(a_{3}=a_{1} + b_{1}+b_{2}\)

：

\(a_{n}=a_{1} + b_{1}+b_{2}+ \cdots +b_{n-1} \)

[/st-mybox]

したがって、階差数列を用いた一般項は

\[a_{n}=a_{1}+\sum_{k=1}^{n-1} b_{k}\]

となります。

階差数列の一般項を求める

ここに数列があります。

3 , 5 , 8 , 12 , 17 , 23 …

この数列だけでは法則が見えませんが、各項の差を求めると

2 , 3 , 4 , 5 , 6 …

階差数列が「初項2、公差1の等差数列」になっています。

ここで階差数列を用いた数列の一般項の公式を思い出しましょう。

[st-mybox title=”階差数列と一般項” fontawesome=”” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

数列\(\{a_{n}\}\)の階差数列を\(\{b_{n}\}\)とすると、n≧2のとき

\[a_{n}=a_{1}+\sum_{k=1}^{n-1} b_{k}\]

[/st-mybox]

もとの数列\(\{a_{n}\}\)は初項3で、階差数列\(\{b_{n}\}\)は「初項2、公差1の等差数列」なので

\[b_{n}=2+(n-1)\]

\(n≧2\)のとき、

\begin{eqnarray}
a_{n}&=&a_{1}+\sum_{k=1}^{n-1} b_{k}\\
&=&3+\sum_{k=1}^{n-1} \{2+(k-1)\}\\
&=&3+\sum_{k=1}^{n-1} (1+k)\\
&=&3+\sum_{k=1}^{n-1} 1+\sum_{k=1}^{n-1} k
\end{eqnarray}

[st-mybox title=”参考” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

ここからΣ（シグマ）の計算をします。

シグマの計算公式を知りたい方は「Σシグマの計算公式と証明！数列の和が一瞬で解ける！」をご覧ください。

[/st-mybox]

\begin{eqnarray}
a_{n}&=&3+\sum_{k=1}^{n-1} 1+\sum_{k=1}^{n-1} k\\
\displaystyle &=&3+(n-1)+\frac{1}{2}(n-1)n\\
\displaystyle &=&\frac{1}{2}n^{2}+\frac{1}{2}n+2\\
\end{eqnarray}

よって、\[\displaystyle a_{n}=\frac{1}{2}n^{2}+\frac{1}{2}n+2\]

\(n=1\)のとき\(a_{1}=3\)となり、初項でも成り立つ。

したがって、与えられた数列の一般項は

\[\displaystyle a_{n}=\frac{1}{2}n^{2}+\frac{1}{2}n+2\]

一般項が不安なときは数字を代入して確かめます。

一般項に\(n=2\)を代入して

\begin{eqnarray}
\displaystyle a_{2}&=&\frac{1}{2}\cdot 2^{2}+\frac{1}{2} \cdot 2+2\\
&=&2+1+2\\
&=&5
\end{eqnarray}

ちゃんと同じ値になったので間違いなさそうです。

階差数列の和

階差数列の和

数列の項を足すことを数列の和といいます。

数列{3 , 5 , 8 , 11}の初項から第4項までの和は27となります。

[st-mybox title=”” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

3+5+8+11=27

[/st-mybox]

このように数列の和を求める問題はよく出題されます。

もとの数列が等差数列か等比数列のときは和の公式があります。

[st-tab-content memo=”数列の和の公式” type=”button” myclass=”st-radius”]
[st-input-tab fontawesome=”” text=”等差数列の和” bgcolor=”” bordercolor=”#B3E5FC” color=”” fontweight=”” checked=”checked”]
[st-input-tab fontawesome=”” text=”等比数列の和” bgcolor=”” bordercolor=”#B3E5FC” color=”” fontweight=”” checked=””]
[st-tab-main bgcolor=”” bordercolor=”#ccc”]

初項\(a\)、公差\(d\)、末項\(l\)、項数\(n\)の等差数列の和を\(S_{n}\)とすると、

\begin{eqnarray}
\displaystyle S_{n}&=&\frac{n}{2}(a+l)\\
\displaystyle &=&\frac{n}{2}\{2a+(n-1)d\}
\end{eqnarray}

[/st-tab-main][st-tab-main bgcolor=”” bordercolor=”#ccc”]

初項\(a\)、公差\(d\)、項数\(n\)の等比数列の和を\(S_{n}\)とすると、

[1]\(r < 1\)のとき

\[\displaystyle S_{n}=\frac{a(1-r^{n})}{1-r}\]

[2]\(r > 1\)のとき

\[\displaystyle S_{n}=\frac{a(r^{n}-1)}{r-1}\]

[3]\(r=1\)のとき

\[S_{n}=na\]

[/st-tab-main]
[/st-tab-content]

[st-mybox title=”参考” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

等差数列の和の公式について知りたい！

等比数列の和の公式について知りたい！

[/st-mybox]

今回は階差数列ですが、上記の公式も確実に覚えておきましょう。

[st-mybox title=”階差数列の和の公式” fontawesome=”” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

数列\(\{a_{n}\}\)の初項から第\(n\)項までの和を\(S_{n}\)とすると、

\[\displaystyle S_{n}=\sum_{k=1}^{n} a_{k}\]

[/st-mybox]

実際に数字を使って和を求めてみましょう。

階差数列の和を求める

このような数列があったとします。

1 , 3 , 7 , 13 , 21 , 31 , 43 …

この数列の階差数列は「初項2、公差2の等差数列」です。

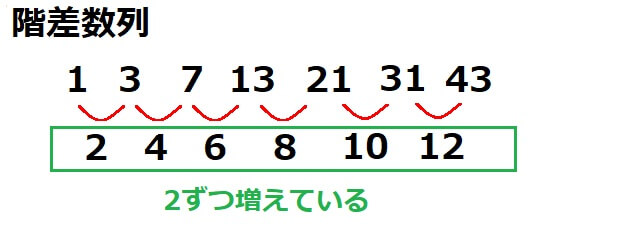
数列の和を求めるには、まず一般項\(\{a_{n}\}\)を求める必要があります。

ここで一般項を求める公式を思い出して、

\begin{eqnarray}
a_{n}&=&1+\sum_{k=1}^{n-1} \{2+2(k-1)\}\\
&=&1+\sum_{k=1}^{n-1} 2k\\
\displaystyle &=&1+2 \cdot \frac{1}{2}(n-1)n\\
&=&n^{2}-n+1
\end{eqnarray}

一般項が分かれば、数列の和を求めることができます。

初項\(\{a_{n}\}\)から第\(n\)項\(\{a_{n}\}\)までの和は、

\begin{eqnarray}
S_{n}&=&\sum_{k=1}^{n} a_{k}\\
&=&\sum_{k=1}^{n} (n^{2}-n+1)\\
&=&\sum_{k=1}^{n} n^{2}-\sum_{k=1}^{n} n+\sum_{k=1}^{n} 1\\
\displaystyle &=&\frac{1}{6}n(n+1)(2n+1)-\frac{1}{2}n(n+1)+n\\
\displaystyle &=&\frac{1}{3}n(n^{2}+2)
\end{eqnarray}

したがって、与えられた数列の初項から第\(n\)項までの和\(S_{n}\)は

\[\displaystyle S_{n}=\frac{1}{3}n(n^{2}+2)\]

階差数列の漸化式

漸化式が\(a_{n+1}=a_{n}+(nの式)\)の形のとき、階差数列を利用して一般項を求めます。

[st-mybox title=”階差数列を利用する漸化式” fontawesome=”” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

数列における第\(n\)項を\(a_{n}\)とするとき

\[a_{n+1}=a_{n}+f(n)\]

式変形をすると

\[a_{n+1}-a_{n}=f(n)\]

これは数列\(\{a_{n}\}\)の階差数列の第\(n\)項が\(f(x)\)であることを表す。

[/st-mybox]

実際に漸化式から一般項を求めてみましょう。

[st-mybox title=”例題1″ fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

次の条件によって定められる数列\(\{a_{n}\}\)の一般項を求めよう。

\[a_{1}=3　a_{n+1}=a_{n}+2^{n}\]

[/st-mybox]

条件より\[a_{n+1}-a_{n}=2^{n}\]

数列\(\{a_{n}\}\)の階差数列の第\(n\)項が\(2^{n}\)なので、

\(n≧2\)のとき

\begin{eqnarray}
a_{n}&=&a_{1}+\sum_{k=1}^{n-1} 2^{k}\\
\displaystyle &=&3 + \frac{2(2^{n-1}-1)}{2-1}
\end{eqnarray}

よって、

\[a_{n}=2^{n}+1\]

\(n=1\)のとき、\(a_{1}=3\)となり初項でも成り立つ。

したがって、一般項は\(a_{n}=2^{n}+1\)

その他の数列

今回は階差数列をメインに解説しています。

数列には階差数列の他にも重要な数列があります。

[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#f3f3f3″ borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

• 等差数列
• 等比数列

[/st-mybox]

・等差数列

等差数列とは、「一定の差で変化する数列」を指します。

等差数列については、「等差数列の公式まとめ！一般項と和の公式を分かりやすく解説！」で詳しく解説しています。

・等比数列

等比数列とは、「初めの項に一定の数をかけ続けていく数列」を指します。

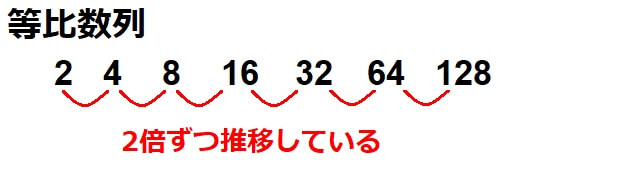
等比数列については、「等比数列の公式まとめ！一般項と和の公式を分かりやすく解説！」で詳しく解説しています。

階差数列《練習問題》

ここまで数列の一般項の求め方や和の求め方について解説してきました。

実際に問題を解いてみて、計算に慣れていきましょう。

[st-mybox title=”練習問題1″ fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

次の数列の一般項を求めよう。

1 , 4 , 9 , 16 , 25 , 36 …

[/st-mybox]

[st-slidebox fontawesome=”” text=” ＋解答” bgcolor=”” color=”#1a1a1a” margin_bottom=”20″]

与えられた数列の階差数列は「初項3、公差2の等差数列」である。

よって、

\[b_{n}=3+2(n-1)=2n+1\]

初項\(a_{1}\)と階差数列\(\{b_{n}\}\)が分かったので一般項を求めることができます。

\(n≧2\)のとき

\begin{eqnarray}
a_{n}&=&1+\sum_{k=1}^{n-1} (2k+1)\\
\displaystyle &=&1+2\sum_{k=1}^{n-1} k +\sum_{k=1}^{n-1} 1\\
\displaystyle &=&1+2 \cdot \frac{1}{2}(n-1)n +(n-1)\\
&=&n^{2}
\end{eqnarray}

すなわち\[a_{n}=n^{2}\]

\(n=1\)のとき\(a_{1}=1\)となり、初項でも成り立つ。

したがって、一般項は\[a_{n}=n^{2}\]

[/st-slidebox]

[st-mybox title=”練習問題2″ fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

次の数列において、初項から第\(n\)項までの和を求めよう。
1　4　13　40　121　…

[/st-mybox]

[st-slidebox fontawesome=”” text=”+ 解答” bgcolor=”” color=”#1a1a1a” margin_bottom=”20″]

まずは一般項\(\{a_{n}\}\)を求める必要がある。

与えられた数列の階差数列は「初項3、公比3の等比数列」なので、

\[b_{n}=3 \cdot 3^{n-1}=3^{n}\]

\(n≧2\)のとき

\begin{eqnarray}
a_{n}&=&1+\sum_{k=1}^{n-1} 3^{k}\\
\displaystyle &=&1+\frac{3(3^{n-1}-1)}{3-1}\\
\displaystyle &=&1+\frac{1}{2}(3^{n}-3)\\
\displaystyle &=&\frac{1}{2}(3^{n}-1)
\end{eqnarray}

\(n=1\)のとき\(a_{1}=1\)となり、初項でも成り立つ。

したがって、一般項は\[\displaystyle a_{n}=\frac{1}{2}(3^{n}-1)\]

これで数列の和を求めることができます。

数列\(\{a_{n}\}\)の初項から第\(n\)項までの和\(S_{n}\)は

\begin{eqnarray}
S_{n}&=&\sum_{k=1}^{n} a_{k}\\
\displaystyle &=&\frac{1}{2} \sum_{k=1}^{n} 3^{k}-\frac{1}{2} \sum_{k=1}^{n} 1\\
\displaystyle &=&\frac{1}{2} \cdot \frac{3(3^{n}-1)}{3-1}-\frac{1}{2} \cdot n\\
\displaystyle &=&\frac{3}{4}(3^{n}-1)-\frac{1}{2}n\\
\end{eqnarray}

したがって、求める数列の和\(S_{n}\)は

\[\displaystyle S_{n}=\frac{3}{4}(3^{n}-1)-\frac{1}{2}n\]

[/st-slidebox]

階差数列まとめ

今回は階差数列について詳しく解説しました。

[st-minihukidashi fontawesome=”fa-check” fontsize=”” fontweight=”100″ bgcolor=”#FFC107″ color=”#fff” margin=”0 0 20px 0″ radius=”” position=”” myclass=”” add_boxstyle=””]階差数列　まとめ[/st-minihukidashi]

階差数列とは
⇒数列\(\{a_{n}\}\)の隣接する項の差を項とする数列

[st-mybox title=”階差数列と一般項” fontawesome=”” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

数列\(\{a_{n}\}\)の階差数列を\(\{b_{n}\}\)とすると、n≧2のとき

\[a_{n}=a_{1}+\sum_{k=1}^{n-1} b_{k}\]

[/st-mybox]

[st-mybox title=”階差数列の和の公式” fontawesome=”” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

数列\(\{a_{n}\}\)の初項から第\(n\)項までの和を\(S_{n}\)とすると、

\[\displaystyle S_{n}=\sum_{k=1}^{n} a_{k}\]

[/st-mybox]

今回は階差数列を中心に解説しましたが、等差数列や等比数列も重要な数列です。

この3つの数列をしっかりと理解していないと、漸化式や群数列でかなり苦戦することになると思います。

それぞれの数列についてはこちら記事で解説しているので、ぜひご覧ください。

[st-midasibox title=”合わせて読みたい” fontawesome=”fa-check-circle faa-ring animated” bordercolor=”#FFC107″ color=”” bgcolor=”#FFFDE7″ borderwidth=”” borderradius=”5″ titleweight=”bold” myclass=””]

等差数列の一般項と和の公式

[st-card myclass=”” id=”3767″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]

等比数列の一般項と和の公式

[st-card myclass=”” id=”3800″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]

[/st-midasibox]

[st-mybutton class=”” url=”https://math-travel.jp/suuretu/” title=”数列のまとめ記事へ” rel=”” fontawesome=”” target=”” color=”#9CCC65″ bgcolor=”” bgcolor_top=”” bordercolor=”#9CCC65″ borderwidth=”3″ borderradius=”30″ fontsize=”” fontweight=”bold” width=”” fontawesome_after=”fa-chevron-right” shadow=”” ref=”” beacon=””]