数学B数列の中でも「等差数列」は必ず理解して欲しい数列です。
[st-mybox title=”今回解決する悩み” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”4″ borderradius=8″ titleweight=”bold” fontsize=”110″ myclass=”nayami-box” margin=”50px auto 40px”]
「等差数列ってなに?」
「等差数列の一般項の求め方は?」
「和の公式を忘れてしまった」
[/st-mybox]
今回は等差数列に関するこんな悩みを解決します。
 高校生
高校生一般項や数列の和がよく分からなくて…
等差数列とは「一定の差で変化していく数列」を指します。

数列を学習するうえで、等差数列は重要な数列の1つです。
等差数列をしっかり理解しておかないと、この先の単元でかなり苦戦することになります。
本記事では等差数列の一般項と和の公式について解説します。
数列が苦手な方や、これから数列を学習する方の参考になるので、ぜひ最後までご覧ください。
 シータ
シータ気になる見出しをクリックして、
ぜひ最後までご覧ください。
[st_af id=”13737″]
等差数列とは?
等差数列とは、「一定の差で変化する数列」を指します。

数列の初めの項を初項、最後の項を末項といいます。

また、等差数列において隣り合う2つの項の差を公差といいます。
以下のような数列があるとします。

この数列は「初項5、末項40、公差7、項数6の等差数列」といいます。
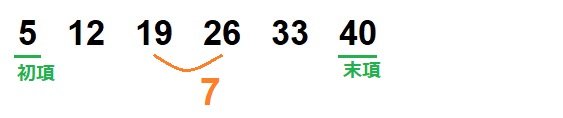
[st-mybox title=”等差数列” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
等差数列 ⇒ 一定の差で変化する数列
公差:隣りあう項の差
初項:最初の項
末項:最後の項
[/st-mybox]
等差数列を一般項で表す
等差数列の一般項の公式
一般項とは、数列の第\(n\)項\(a_{n}\)を\(n\)を用いて表したものです。
等差数列の一般項は以下の公式で表します。
[st-mybox title=”等差数列の一般項” fontawesome=”” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
初項\(a_{1}\)、公差\(d\)の等差数列を\(\{a_{n}\}\)とすると、
\(a_{n}=a_{1} + (n-1)d\)
[/st-mybox]
 高校生
高校生なんだか難しい形をしているね…
 シータ
シータ公式の証明を見れば、この形になるのも納得できるよ!
等差数列の一般項の証明
等差数列は初項に公差を加えていく数列です。
数列\(a_{1} a_{2} a_{3} a_{4} … a_{n}\)が等差数列だとします。
この等差数列の公差を\(d\)とすると、
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a_{1}=a_{1}\)←初項
\(a_{2}=a_{1} + d\)
\(a_{3}=a_{1} + 2d\)
\(a_{4}=a_{1} + 3d\)
[/st-mybox]
このように初項に公差を加えていくので、
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(a_{1}=a_{1}\)
\(a_{2}=a_{1} + d\)
\(a_{3}=a_{1} + 2d\)
:
\(a_{n}=a_{1} + (n-1)d\)
[/st-mybox]
したがって、等差数列の一般項は\(a_{n}=a_{1} + (n-1)d\)となります。
 シータ
シータ具体的な数字を使って一般項を考えてみよう!
等差数列の一般項を求める
ここに等差数列があります。
3 , 7 , 11 , 15 , 19 , 23 ,27 …
この数列は「初項3、公差4の等差数列」です。
ここで等差数列の一般項の公式を思い出しましょう。
[st-mybox title=”等差数列の一般項” fontawesome=”” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
初項\(a_{1}\)、公差\(d\)の等差数列を\(\{a_{n}\}\)とすると、
\(a_{n}=a_{1} + (n-1)d\)
[/st-mybox]
この数列は\(a_{1}=3、d=4\)の等差数列なので求める一般項は、
\begin{eqnarray}
a_{n}&=&a_{1}+(n-1)d\\
&=&3+(n-1)4\\
&=&4n-1
\end{eqnarray}
したがって、等差数列{3 , 7 , 11 , 15 , 19 …}の一般項は\(a_{n}=4n-1\)
 シータ
シータ心配なときは代入して確かめてみよう!
一般項が不安なときは具体的な数字を代入して確かめます。
初項が3なので、一般項に\(n=1\)を代入して3にならないとおかしいです。
\begin{eqnarray}
a_{1}&=&4 \times 1-1\\
&=&3
\end{eqnarray}
ちゃんと同じ値になったので間違いなさそうです。
等差数列の和
等差数列の和の公式
数列の項を足すことを数列の和といいます。
等差数列{2 , 5 , 8 , 11}の初項から第4項までの和は26となります。
[st-mybox title=”” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
2+5+8+11=26
[/st-mybox]
このように等差数列の和を求める問題はよく出題されます。
等差数列の和を求める公式が2つあります。これは確実に覚えておきたい公式です。
[st-mybox title=”等差数列の和” fontawesome=”” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
初項\(a\)、公差\(d\)、末項\(l\)、項数\(n\)の等差数列の和を\(S_{n}\)とすると、
\begin{eqnarray}
\displaystyle S_{n}&=&\frac{n}{2}(a+l)\\
\displaystyle &=&\frac{n}{2}\{2a+(n-1)d\}
\end{eqnarray}
[/st-mybox]
実際に等差数列の和を2つのやり方で求めてみます。
等差数列の和の公式①
このような等差数列があったとしましょう。

これは初項5、末項40、項数6の等差数列です。
初項と末項が分かっているときはこっちの和の公式を使いましょう。
[st-mybox title=”等差数列の和” fontawesome=”” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
初項\(a\)、末項\(l\)、項数\(n\)の等差数列の和を\(S_{n}\)とすると、
\begin{eqnarray}
\displaystyle S_{n}&=&\frac{n}{2}(a+l)\\
\end{eqnarray}
[/st-mybox]
この数列の初項から第6項までの和は
\begin{eqnarray}
\displaystyle S_{6}&=&\frac{6}{2}(5+40)\\
&=&3 \times 45\\
&=&135
\end{eqnarray}
したがって、等差数列の和を求めることができました。
[st-mybox title=”等差数列の和の公式” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#FFFDE7″ borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
初項、末項、項数が分かる場合はこの公式で求める。
\begin{eqnarray}
\displaystyle S_{n}&=&\frac{n}{2}(a+l)
\end{eqnarray}
[/st-mybox]
等差数列の和の公式②
同じ等差数列の和をもう1つの求め方で求めましょう。

この数列は初項5、公差7、項数6の等差数列です。
初項、公差、項数が分かっているときはこの公式を使います。
[st-mybox title=”等差数列の和” fontawesome=”” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
初項\(a\)、公差\(d\)、項数\(n\)の等差数列の和を\(S_{n}\)とすると、
\begin{eqnarray}
\displaystyle S_{n}&=&\frac{n}{2}\{2a+(n-1)d\}
\end{eqnarray}
[/st-mybox]
この数列の初項から第6項までの和は
\begin{eqnarray}
\displaystyle S_{6}&=&\frac{6}{2}(2 \times 5+(6-1)7)\\
&=&3 (10 + 35)\\
&=&3 \times 45\\
&=&135
\end{eqnarray}
\(\displaystyle S_{6}=\frac{6}{2}\{2 \times{5}+(6-1)\times{7}\}\)
\(\displaystyle =3(10 + 35)\)
\(=135\)
したがって、等差数列の和を求めることができました。
[st-mybox title=”等差数列の和の公式” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#FFFDE7″ borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
初項、公差、項数が分かる場合はこの公式で求める。
\begin{eqnarray}
\displaystyle S_{n}&=&\frac{n}{2}\{2a+(n-1)d\}
\end{eqnarray}
[/st-mybox]
等差数列のΣ
そもそもΣ(シグマ)とは?
Σ(シグマ)とは数学の記号の1つです。
数列\(a_{n}\)の初項から第\(n\)項まで足すことを記号Σ(シグマ)を用いて、以下のように表します。
[st-mybox title=”” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\[\sum_{k=1}^{n} a_{k}=a_{1}+a_{2}+a_{3}+\cdots+a_{n}\]
[/st-mybox]
\(\sum_{k=1}^{n}\)の見た目が難しそうなので身構えてしまいますが、シグマの意味は「k=1からnまで代入したものを足す」というだけです。
シグマΣの公式や計算については「Σシグマの計算公式と証明!数列の和が一瞬で解ける!」で解説しています。
等差数列のΣ
次のようなΣは、等差数列の和として考えることができます。
[st-mybox title=”等差数列のΣ” fontawesome=”” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\[\sum_{k=1}^{n} k=\displaystyle \frac{1}{2}n(n+1)\]
[/st-mybox]
なぜこの公式になるのかを解説します。
まず左辺のΣを計算してみると、
\[\sum_{k=1}^{n} k=1+2+3+ \cdots + n\]
となります。
これは「初項1、末項n、項数nの等差数列の和」と同じ形ですね。
そこで等差数列の和の公式を用いると、
\begin{eqnarray}
\sum_{k=1}^{n} k&=&1+2+3+ \cdots + n\\
\displaystyle &=&\frac{1}{2}n(n+1)
\end{eqnarray}
これで等差数列のΣを和の公式で表すことができました。
等差数列のΣを求める
例題として、1問Σの計算をしてみましょう。
[st-mybox title=”等差数列のΣ” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
次の値を求めてみよう。
\[\sum_{k=1}^{7} k\]
[/st-mybox]
この計算が意味するのは、\(1+2+3+\cdots+7\)なので、「初項1、末項7、項数7の等差数列の和」として考えると、
\begin{eqnarray}
\sum_{k=1}^7 k&=&1+2+3+ \cdots + 7\\
\displaystyle &=&\frac{1}{2}7(7+1)\\
\displaystyle &=&28
\end{eqnarray}
Σの計算公式を知らないと、和\(S_{n}\)や群数列で苦戦することになります。
[st-card myclass=”” id=”3817″ label=”おすすめ” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]
等差数列の漸化式
等差数列の漸化式は以下のような形になります。
[st-mybox title=”等差数列の漸化式” fontawesome=”fa-question-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
数列における第\(n\)項を\(a_{n}\)、公差をdとすると
\(a_{n+1}=a_{n}+d\)
[/st-mybox]
漸化式とは、数列の第\(n\)項\(a_{n}\)を用いて次の項\(a_{n+1}\)を表す式です。
等差数列の漸化式は、\(a_{n}\)に公差dを加えると\(a_{n+1}\)になることを表しています。
実際に数字を入れて考えてみましょう。

これは初項2、公差3の等差数列です。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
つまり、
\(a_{1}=2\)
\(a_{2}=a_{1}+3\)
\(a_{3}=a_{2}+3\)
\(a_{4}=a_{3}+3\)
という関係が成り立ちます。
[/st-mybox]
したがって、第\((n+1)\)項を表すときは第\(n\)項に3を加えればよいので
\[a_{n+1}=a_{n}+3\]
よって、等差数列の漸化式は以下の形で表される。
[st-mybox title=”ポイント” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#FFFDE7″ borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
数列における第\(n\)項を\(a_{n}\)、公差をdとすると
\(a_{n+1}=a_{n}+d\)
[/st-mybox]
等差数列の性質
等差数列の性質の1つに”等差中項”というものがあります。
[st-mybox title=”等差中項” fontawesome=”” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
数列\(a,b,c\)が等差数列のとき、
\[2b=a+c\]
[/st-mybox]
これは等差数列の項3つ用意したときに、両端の項の和が中央の項の2倍になることを意味します。
証明は非常に簡単です。\(a,b,c\)は等差数列なので
\(b-a=c-b\)
各項を移行すると、
\(2b=a+c\)
となります。
その他の数列
今回は等差数列について解説しています。
数列には等差数列以外にも以下の数列があります。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#f3f3f3″ borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 等比数列
- 階差数列
[/st-mybox]
・等比数列
等比数列とは、「初めの項に一定の数をかけ続けていく数列」を指します。
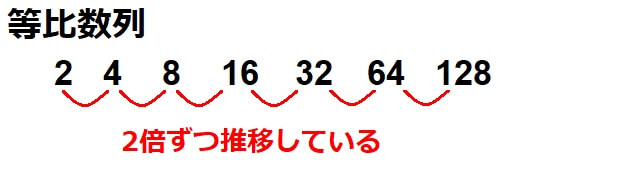
等比数列については、「等比数列の公式まとめ!一般項と和の公式を分かりやすく解説!」で詳しく解説しています。
・階差数列
階差数列は複雑で、各項の差を書き出してみるとある数列が見えてきます。
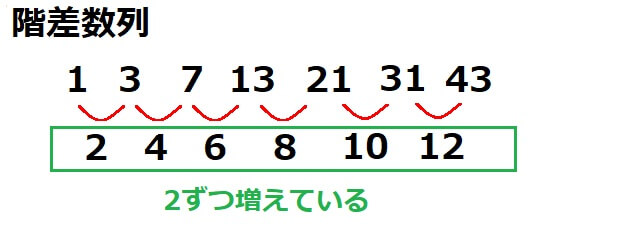
上の数列の場合、各項の差が等差数列になっています。
この差が等比数列になる場合もありますし、もっと複雑な数列になるときもあります。
階差数列については、「階差数列を用いた一般項と和を求める公式!初項に階差を足していくだけ」で解説しています。
等差数列《練習問題》
ここまで等差数列の一般項や和の公式について解説しました。
実際に、数字をつかって練習問題に挑戦してみましょう。
[st-mybox title=”練習問題1″ fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
次の数列の一般項を求めよう。
5 , 9 , 13 , 17 , 21 , 25 …
[/st-mybox]
+ 解答
与えられた数列は「初項5、公差4の等差数列」です。
したがって、求める一般項は
\begin{eqnarray}
a_{n}&=&5+(n-1)4\\
&=&4n+1
\end{eqnarray}
[st-mybox title=”練習問題2″ fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
等差数列において、初項から第\(n\)項までの和を求めよう。
3 7 11 15 19 23 …
[/st-mybox]
[st-slidebox fontawesome=”” text=”+ 解答” bgcolor=”” color=”#1a1a1a” margin_bottom=”20″]
これは「初項3、公差4、項数nの等差数列の和」です。
等差数列の和の公式に代入して
\begin{eqnarray}
\displaystyle S_{n} &=&\frac{n}{2}\{2a_{1}+(n-1)d\}\\
\displaystyle &=&\frac{n}{2}\{2 \cdot 3+4(n-1)\}\\
\displaystyle &=&\frac{n}{2}(4n+2)\\
&=&2n^{2}+n
\end{eqnarray}
したがって、求める和は
\(S_{n}=2n^{2}+n\)
[/st-slidebox]
等差数列 まとめ
今回は等差数列について詳しく解説しました。
[st-minihukidashi fontawesome=”fa-check” fontsize=”” fontweight=”100″ bgcolor=”#FFC107″ color=”#fff” margin=”0 0 20px 0″ radius=”” position=”” myclass=”” add_boxstyle=””]等差数列 まとめ[/st-minihukidashi]
等差数列とは
⇒一定の差で変化する数列
[st-mybox title=”等差数列の一般項” fontawesome=”” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
初項\(a_{1}\)、公差\(d\)の等差数列を\(\{a_{n}\}\)とすると、
\(a_{n}=a_{1} + (n-1)d\)
[/st-mybox]
[st-mybox title=”等差数列の和” fontawesome=”” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
初項\(a\)、公差\(d\)、末項\(l\)、項数\(n\)の等差数列の和を\(S_{n}\)とすると、
\begin{eqnarray}
\displaystyle S_{n}&=&\frac{n}{2}(a+l)\\
\displaystyle &=&\frac{n}{2}\{2a+(n-1)d\}
\end{eqnarray}
[/st-mybox]
今回は等差数列に焦点を当てて解説しましたが、等比数列や階差数列も重要な数列です。
この3つの数列をしっかりと理解していないと、漸化式や群数列でかなり苦戦することになると思います。
それぞれの数列についてはこちら記事で解説しているので、ぜひご覧ください。
[st-midasibox title=”合わせて読みたい” fontawesome=”fa-check-circle faa-ring animated” bordercolor=”#FFC107″ color=”” bgcolor=”#FFFDE7″ borderwidth=”” borderradius=”5″ titleweight=”bold” myclass=””]
等比数列の一般項と和の公式
[st-card myclass=”” id=”3800″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]
階差数列の一般項と漸化式
[st-card myclass=”” id=”6221″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]
[/st-midasibox]
[st-mybutton class=”” url=”https://math-travel.jp/suuretu/” title=”数列のまとめ記事へ” rel=”” fontawesome=”” target=”” color=”#9CCC65″ bgcolor=”” bgcolor_top=”” bordercolor=”#9CCC65″ borderwidth=”3″ borderradius=”30″ fontsize=”” fontweight=”bold” width=”” fontawesome_after=”fa-chevron-right” shadow=”” ref=”” beacon=””]
[st_af id=”4202″]

