数学Bでは「数列」が多くの高校生を苦しめます。
[st-mybox title=”今回解決する悩み” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”4″ borderradius=8″ titleweight=”bold” fontsize=”110″ myclass=”nayami-box” margin=”30px auto 40px”]
「数列ってなに?」
「数列の基本から分からなくて」
[/st-mybox]
今回は数列に関するこんな悩みを解決していきます。
 高校生
高校生数列ってなんだか難しそう…
“数列”とは一定の法則で並ぶ数字の列を指します。
そんな数列にもいろいろな種類があって、今回は重要な数列を3つ紹介します。
[st-mybox title=”数列の種類” fontawesome=”” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#f3f3f3″ borderwidth=”1″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
- 等差数列
- 等比数列
- 階差数列
[/st-mybox]
本記事では数列の基本となる知識や用語を解説します。
数列が苦手な方や、これから数列を学習する方の参考になるのでぜひ最後までご覧ください。
 シータ
シータ気になる見出しをクリックして、
ぜひ最後までご覧ください。
[st_af id=”13737″]
数列とは?

数列とは上のように数字を一列に並べたものをいいます。
この数字はランダムに並べているのではなく、並び方にはある法則があります。
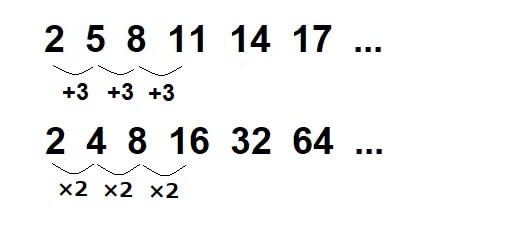
上の数列のように、同じ差で変化していく数列を等差数列といいます。
一方で、下の数列のように同じ比を掛けていく数列を等比数列といいます。
数列の種類については、このあと詳しく解説します。
数列の基本用語
数列のなかの数字1つ1つを項といいます。


数列の最初の項を初項と呼び、最後の項を末項と呼びます。
[st-mybox title=”数列の項” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
数列のなかでも以下の項には別の呼び方があります。
最初の項 ⇒ 初項(しょこう)
最後の項 ⇒ 末項(まっこう)
[/st-mybox]
 高校生
高校生始まりが初項、終わりが末項というんだね
 シータ
シータここで紹介した用語はずっと使う言葉だから、必ず理解しておこう!
数列の3つの基本の型
数列にもいくつか種類があります。
その中でも基本となる3つの数列を紹介します。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#f3f3f3″ borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
[/st-mybox]
等差数列

項が進むにつれて一定の差で変化する数列を「等差数列」といいます。
等差数列の各項の差を公差と呼びます。
今回の例だと3ずつ増えているので、公差は3ということになります。
ちなみに、この数列は「初項が3、末項が20、公差3の等差数列」と表現します。
等比数列
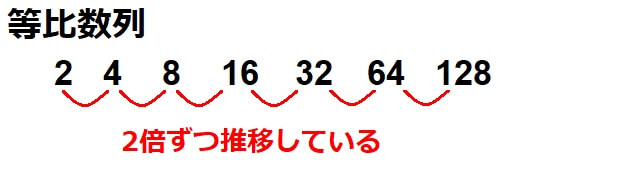
一定の比で変化している数列を「等比数列」といいます。
各項に掛けていく値を公比といいます。
今回の例だと、2倍ずつ変化しているので公比2となります。
よって、この数列を「初項2、末項128、公比2の等比数列」と呼びます。
階差数列
階差数列はその法則に気が付きにくいです。
各項の差を書き出してみると、その差にある法則が見えてきます。
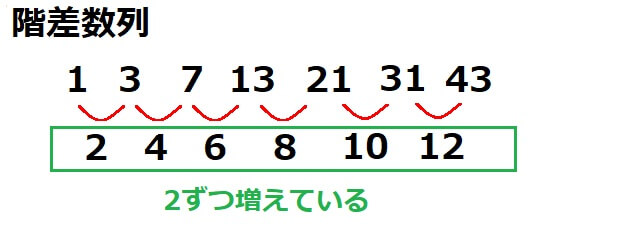
上の数列の場合、各項の差が等差数列になっています。
この差が等比数列になる場合もありますし、もっと複雑な数列になるときもあります。
数列の一般項とは?
数列の並びを\(n\)を用いて一般化したものを一般項と呼びます。
 シータ
シータ一般項がよく分からずに、数列が苦手になる人が多いよ
一般項について解説します。
ここに初項が2、第2項が4、第3項が6、…の数列があります。

数列の法則を見つけて、1つの式で表したものを一般項といいます。
この数列の第n項を\(a_{n}\)とすると、\(a_{n}\)には\(a_{n}=2n\)の関係があることに気が付きます。
[st-mybox title=”” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#f3f3f3″ borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
初項 2×1=2
第2項 2×2=4
第3項 2×3=6
第4項 2×4=8
:
第n項 2×n=2n
[/st-mybox]
したがって、下の数列の一般項は\(a_{n}=2n\)となります。

 高校生
高校生法則を見つけるなんて難しそう…
 シータ
シータ慣れてきたらすぐに分かるのと、実は数列の種類によって一般項の型があるんだ
数列の一般項や漸化式については以下の記事でまとめて解説しています。
[st-card myclass=”” id=”6197″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]
数列の種類《練習問題》
数列の種類を解説したので、次の数列がどのタイプの数列か考えてみましょう。
[st-mybox title=”練習問題①” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
以下の数列はなに数列でしょう。
3 , 9 , 27 , 81 , 243 , 729 …
[/st-mybox]
これは初項が3で、次の項に進むにつれて3倍ずつ変化していることに気づければ
『初項3、公比3の等比数列』であることが分かります。
[st-mybox title=”練習問題②” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
1 , 3 , 6 , 10 ,15, 21 , …
[/st-mybox]
この数列の変化は、一定の差でも一定の比でもありません。
そこで、階差数列を疑って各項の差を求めてみましょう。
[st-mybox title=”” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
すると、各項の差が
2 , 3 , 4 , 5 , 6 , … という
初項2、公差1の等差数列になっていました。
[/st-mybox]
つまり、各項の差が数列になっているので、今回与えられた数列は『階差数列』であることが分かりました。
数列の基本 まとめ
今回は数列の基本となる知識をまとめました。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”” bgcolor=”#FFFDE7″ borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=””]
数列とは?
ある法則で並んだ数字の列
数列の重要用語
項:数列のなかの1つ1つの数字
初項:数列の最初の項
末項:数列の最後の項
数列の3つの種類
| 数列の種類 | どんな数列 |
| 等差数列 | 一定の差で変化していく数列 |
| 等比数列 | 一定の比で変化していく数列 |
| 階差数列 | 各項の差が数列になっている数列 |
数列の一般項とは?
数列の各項を\(n\)を用いて1つの式で表したもの。
下の数列の一般項は\(a_{n}=2n\)となる。

[/st-mybox]
数学Bは数列とベクトルが主な単元です。
なのでどちらか1つでも苦手になると、数Bは苦しくなります。
数列は覚えることは少ないので、まずは正しく用語や解き方を理解しましょう。
そのあとはたくさん問題を解いて、いろいろなパターンに慣れていくだけです。
各数列について詳しくまとめたので、ぜひご覧ください。
[st-card myclass=”” id=”3767″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]
[st-card myclass=”” id=”3800″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”” thumbnail=”on” type=””]
[st-mybutton class=”” url=”https://math-travel.jp/suuretu/” title=”数列のまとめ記事へ” rel=”” fontawesome=”” target=”” color=”#9CCC65″ bgcolor=”” bgcolor_top=”” bordercolor=”#9CCC65″ borderwidth=”3″ borderradius=”30″ fontsize=”” fontweight=”bold” width=”” fontawesome_after=”fa-chevron-right” shadow=”” ref=”” beacon=””]

