今回解決する悩み
「3次式の因数分解が知りたい」
「因数分解の具体例が見たい」
3次式の展開公式があるならば、逆は因数分解公式になります。
因数分解の公式を覚えておけば、展開もできるようになるのでぜひ押さえておきましょう。
今回は因数分解の公式について紹介します。
本記事でしっかりと理解しておきましょう！
・3次式の因数分解の公式
・因数定理と使った因数分解
3次式の因数分解
展開公式の逆が因数分解なので、展開の公式を利用すると、因数分解の公式がみえます。
展開したり、因数分解したりスムーズに式変形できるようになると良いですね。
\(a^3-b^3=(a-b)(a^2+ab+b^2)\)
\(a^3+3a^2b+3ab^2+b^3=(a+b)^3\)
\(a^3-3a^2b+3ab^2-b^3=(a-b)^3\)
例題を２つ用意しました。
(1)\(x^3+27\)
\(=x^3+3^3\)
\(=(x+3)(x^2-3x+3)\)
(2)\(x^3-9x^2y+27xy^2-27y^3\)
\(=x^3+3x^2(-3y)+3x(-3y)^2+(-3y)^3\)
\(=(x-3y)^3\)
3次式の因数分解 補題
3次式の因数分解の公式を用いると、こんな問題も解くことができます。
\(=(x^2)^3-(4y^2)^3\)
\(=(x^2-4y^2)\{(x^2)^2+x^2\times(4y^2)+(4y^2)^2\}\)
\(=(x^2-4y^2)(x^4+4x^2y^2+16y^4)\)
\((2)a^6-1\)
\(=(a^2)^3-(1^2)^3\)
\(=(a^2-1^2)\{(a^2)^2+a^2\times(1^2)+(1^2)^2\}\)
\(=(a^2-1)(a^4+a^2+1)\)
因数定理を使った因数分解
次は因数定理を使って因数分解するパターンです。
これは公式と呼べる決まった型がないので、手順を理解しましょう。
- \(P(a)=0\)となる\(a\)を見つける
- \((x-a)\)で\(P(x)\)を割る
①\(P(a)=0\)となる\(a\)を見つける
\(x\)に何を代入したら等式が成り立つかを考えます。
例えば以下のような3次式を因数分解する場合
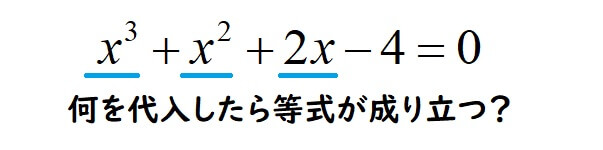
まず等式が成り立つxの値を考えます。
この例題では、\(x=1\)で等式が成り立つことが分かりました。
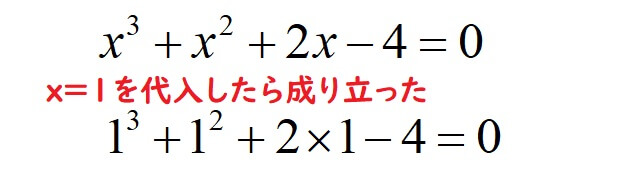
②\((x-a)\)で\(P(x)\)を割る
次に見つけた解を用いて、\(x-1\)で元の式を割ります。
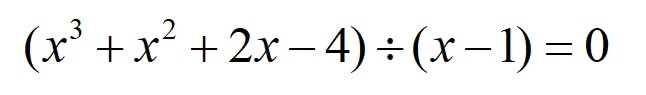
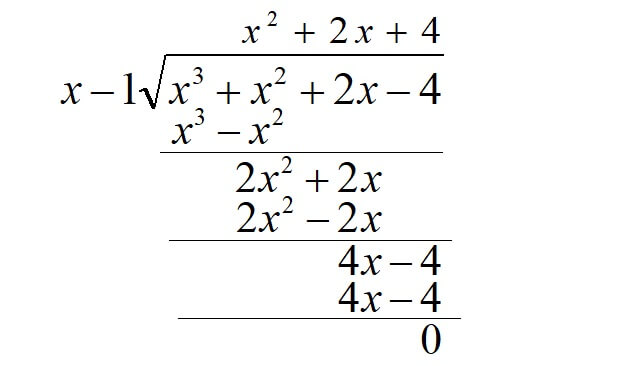
これで因数定理を使った因数分解をすることができました。
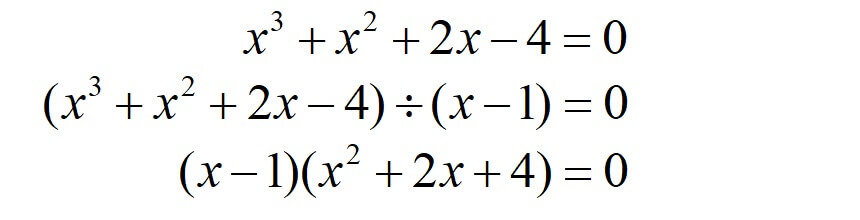
3次式の因数分解 まとめ
今回は3次式の因数分解についてまとめました。
\(a^3-b^3=(a-b)(a^2+ab+b^2)\)
\(a^3+3a^2b+3ab^2+b^3=(a+b)^3\)
\(a^3-3a^2b+3ab^2-b^3=(a-b)^3\)
- \(P(a)=0\)となる\(a\)を見つける
- \((x-a)\)で\(P(x)\)を割る
他にも、教科書に内容に沿った解説記事を挙げています。
お気に入り登録して定期試験前に確認してください。
最後まで読んでくださりありがとうございました。
みんなの努力が報われますように！
コメント