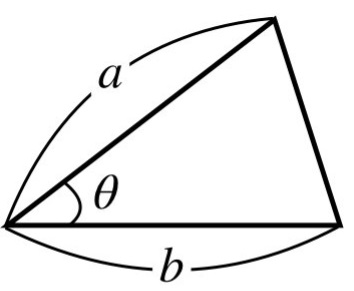
sinθを用いて、三角形の面積を導出します。
各辺の長さと角度を入力後、算出ボタンをクリックしてください。
三角形の面積の公式
12ab sinθ
= 12×より、
入力は0以外を入力してください。
数学Ⅰ三角比のなかで「sinを用いた三角形の面積公式」が登場します。
「三角形の面積公式が知りたい」
「sinの使い方がイマイチわからない」
 高校生
高校生sinを使った面積公式を教えて欲しいです…
三角比には様々な公式がありますが、下図のsinを使った三角形の面積公式は重要な公式の1つです。
[st-mybox title=”三角形の面積公式” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
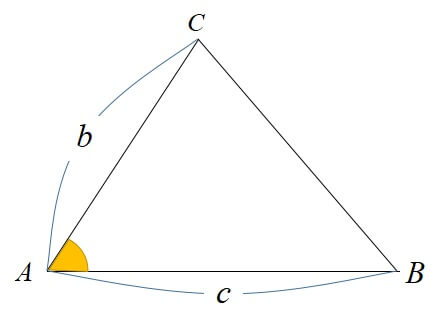 △ABCにおいて2辺の長さを\(a, b\) とするとき、△ABCの面積\(S\)は以下の公式で求めることができる。
△ABCにおいて2辺の長さを\(a, b\) とするとき、△ABCの面積\(S\)は以下の公式で求めることができる。
\begin{eqnarray}
S &=& \frac{1}{2} b c \sin A \\
&=& \frac{1}{2} c a \sin B \\
&=& \frac{1}{2} a b \sin C
\end{eqnarray}
[/st-mybox]
「公式は分かったけど使い方がイマイチで…」
こんな方のために本記事では三角形の面積公式の使い方や例題を交えながら解説していきます。
基礎から確認していくので安心してぜひ最後までご覧ください!
三角比sinで三角形の面積を求める
三角比sinを用いた三角形の面積公式は“三角形の2辺の長さとその間の角の大きさ”が分かってるときに使うことができます。
[st-mybox title=”三角形の面積公式” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
 △ABCにおいて2辺の長さを\(a, b\) とするとき、△ABCの面積\(S\)は以下の公式で求めることができる。
△ABCにおいて2辺の長さを\(a, b\) とするとき、△ABCの面積\(S\)は以下の公式で求めることができる。
\begin{eqnarray}
S &=& \frac{1}{2} b c \sin A \\
&=& \frac{1}{2} c a \sin B \\
&=& \frac{1}{2} a b \sin C
\end{eqnarray}
[/st-mybox]
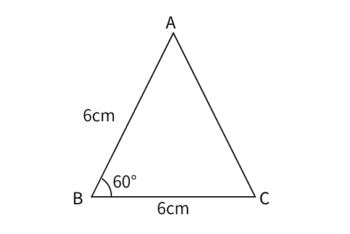
上のような三角形の場合、以下のような式で面積を求める。
\[\displaystyle S=\frac{1}{2} \cdot 6 \cdot 6 \cdot sin60^\circ\]
これを計算して
\begin{eqnarray}
\displaystyle S&=&\frac{1}{2} \cdot 6 \cdot 6 \cdot sin60^\circ\\
\displaystyle &=&\frac{1}{2} \cdot 6 \cdot 6 \cdot \frac{\sqrt{3}}{2}\\
\displaystyle &=&9 \sqrt{3}
\end{eqnarray}
このようにして三角形の面積を求めることができる。
 高校生
高校生2つの辺で挟んで公式に代入するだけですね!
三角形の面積公式 証明
公式を覚えておくのも大切ですが、なぜこの公式が成り立つのか理解しておくことも同じくらい大切です。
三角比sinを用いた面積公式の証明を解説していきます!
△ABCにおいて、角Cから辺ABに垂線を引き、垂線と辺ABの交点をHとする。
すると△ACHができる。
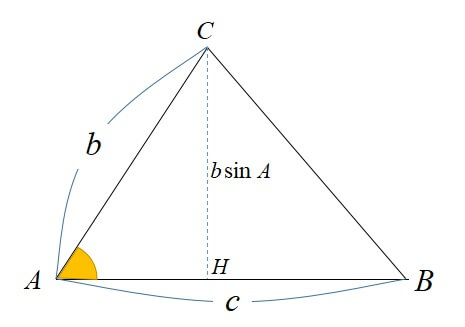
\(\displaystyle sin A=\frac{CH}{AC}=\frac{CH}{b}\)
なので、
\(CH=b sin A\)
三角形の面積は「底辺×高さ÷2」でしたね。
したがって、三角形の面積をSとすると以下が成り立つ。
\(\displaystyle S=\frac{1}{2}bcsinA\)
これは\(\angle B、\angle C\)においても同じことが言えるため、三角形の面積公式が成り立つ。
sinを用いる面積公式<練習問題>

今回学んだ面積公式を用いて練習問題を解いてみましょう。
[st-mybox title=”三角形の面積公式①” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
△ABCにおいて、\(AB=3, AC=5, \angle A=60^\circ\)の時、△ABCの面積を求めよ。
[/st-mybox]
解説
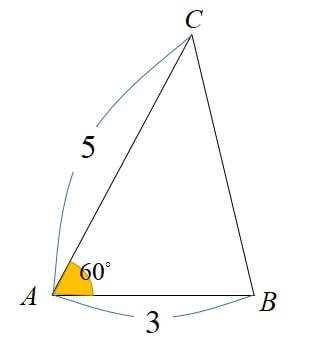
sinを用いた三角形の面積公式より、
\begin{eqnarray}
\displaystyle S&=&\frac{1}{2}bcsinA
\displaystyle &=&\frac{1}{2} \times 5 \times 3 \times \frac{\sqrt{3}}{2}
\displaystyle &=&\frac{15\sqrt{3}}{4}
\end{eqnarray}
[st-mybox title=”三角形の面積公式②” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
△ABCにおいて\(AB=3, AC=6 \)として、 △ABCの面積が\(\displaystyle \frac{9}{2}\)のとき\(\theta\)の値を求めよ。ただし、\(90^\circ < \theta <180^\circ\)とする。
[/st-mybox]
解説
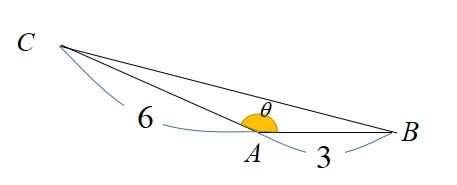
これは面積がすでに分かっているタイプの応用問題です。
\begin{eqnarray}
\displaystyle S&=&\frac{1}{2}bcsinA\\
\displaystyle \frac{9}{2}&=&\frac{1}{2} \cdot 6 \cdot 3 \cdot sinA\\
\displaystyle \frac{9}{2}&=&9 \cdot sinA
\end{eqnarray}
つまり、
\[\displaystyle sinA=\frac{1}{2}\]
となり、\(90^\circ < \theta <180^\circ\)なので、
\(\theta =150^\circ\)と求めることができる。
三角比sinの面積公式 まとめ
今回は数学Ⅰの三角比からsinを用いた三角形の面積公式についてまとめました。
[st-mybox title=”三角形の面積公式” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
 △ABCにおいて2辺の長さを\(a, b\) とするとき、△ABCの面積\(S\)は以下の公式で求めることができる。
△ABCにおいて2辺の長さを\(a, b\) とするとき、△ABCの面積\(S\)は以下の公式で求めることができる。
\begin{eqnarray}
S &=& \frac{1}{2} b c \sin A \\
&=& \frac{1}{2} c a \sin B \\
&=& \frac{1}{2} a b \sin C
\end{eqnarray}
[/st-mybox]
それでは最後まで見ていただいてありがとうございました。
みんなの努力が報われますように!

