入力した関数を微分します。
関数を入力後に算出ボタンクリックしてください。
関数:を微分すると、
になります。
今回は数学Ⅱの微分積分から「\(x^{n}\)の微分」に関するこんな悩みを解決します。
「微分のやり方が分からない」
「微分の公式をまとめて欲しい」
 高校生
高校生微分法を習い始めたばかりで…
微分を活用するとグラフの形や直線の傾きなどを求めることができます。
今後、微分を使いこなしていくためにも、微分の基本公式の理解は必須です。
\[(x^{n})^ \prime =n x^{n-1}\]
指数の\(n\)が係数として前に降りてきて、指数の値は1小さくします。
この記事では微分の超基本となる公式を紹介し、実際に微分のやり方を解説していきます。
とても重要なところなのでしっかり理解できるようにしていきましょう!
\(x^{n}\)べき関数の微分
\(x^{n}\)を微分すると以下のようになります。
\[(x^{n})^ \prime =n x^{n-1}\]
例として\(f(x)=x^{3}\)という式を微分すると
\begin{eqnarray}
f^{\prime} (x)&=&(x^{3})^{\prime}\\
&=&3x^{2}
\end{eqnarray}
このようになります。
合わせて、微分とは何かを説明しておくと、
関数\(f(x)\)から導関数\(f^{\prime} (x)\)を求めることを、\(f(x)\)を\(x\)で微分するまたは単に微分するという。
つまり、
微分する=導関数を求める
ということです。
\(x^{n}\)の微分公式 証明
ここからは、\(x^{n}\)の微分の公式・証明を紹介していきます。
\(x^{n}\)の微分の公式はこれから微分の計算をするときに非常に重要な公式です。
しっかり覚えて使えるようにしていきましょう!
\[(x^{n})^ \prime =n x^{n-1}\]
では実際にこの公式の証明を紹介していきたいと思います。
【証明】
導関数の定義より、
\[x^{n}=\lim_{h \to 0} {\frac{{(x+h)}^n-x^n}{h}}\]
二項定理より、
\((x+h)^{n}\)
\(=nC_{0} x^{n}+nC_{1} x^{n-1} h+\cdots+nC_{n} h^{n}\)
\(=x^{n}+{nx}^{n-1}h+\cdots+h^{n}\)
よって、
\[(x+h)^{n}-x^{n}={nx}^{n-1}h+\cdots+h^{n}\]
両辺を0でない数\(h\)で割ると
\[\displaystyle \frac{(x+h)^{n}-x^{n}}{h}={nx}^{n-1}+\cdots+h^{n-1}\]
したがって、
\[\displaystyle \lim_{h \to 0} {\frac{(x+h)^{n}-x^{n}}{h}}={nx}^{n-1}\]
すなわち
\[(x^{n})^{\prime}={nx}^{n-1}\]
 高校生
高校生二項定理を用いて証明できるんですね!
 シータ
シータ数学は分野を超えて繋がっているんだね
\(x^{n}\)の微分《練習問題》
ここからは、実際に\(x^{n}\)の微分の練習問題を解いていきましょう!
次の関数を微分しなさい。
(1) \(f(x)=x^{4}\)
(2) \(f(x)=x^{5}\)
解答を確認する
(1) \(f^{\prime}(x)=4x^{3}\)
(2) \(f^{\prime}(x)=5x^{4}\)
(1)(2)をまとめて解説していきます。
この問題は両方とも公式に当てはめて計算すればできるのですが、覚えやすい考え方を紹介したいと思います。図を載せておきますので、それを見ながら考えてみてください。
微分の手順
- 微分した関数の係数を考える
- 微分した関数の指数を考える
(1)の問題を使って説明していきます。
\(f(x)=x^{4}\) を微分したとき、xの係数1と指数4をかけた値が微分した関数の係数4になります。
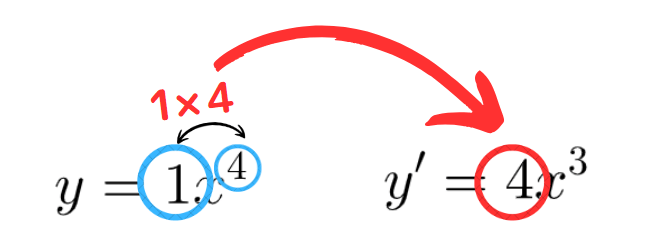
次に手順2です。元の関数の指数4から1を引いた数3が微分した関数の指数となります。
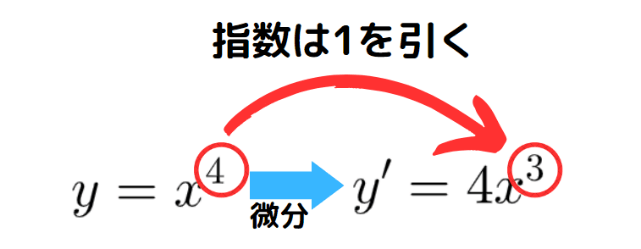
微分は係数と指数、この2つを考えれば終わりです。意外と簡単ですよね。
微分の重要公式
今回は微分の基本となる\(x^{n}\)の微分を中心に解説していますが、微分には必ず覚えておきたい公式がいくつかあります。
 シータ
シータどれも必須だから必ず覚えよう!
定数倍の微分
\(y=k f(x)\)を微分すると、
\[y^{\prime}=k f^{\prime}(x)\]
つまり、定数部分は変わらず\(x\)を持つ部分のみが微分されます。
\(y=3{x}^{2}\)を微分しなさい。
\(x^{n}\)と同じように微分していきます。
指数を前に持ってきて、指数の数字は1下げると
\[y^{\prime}=6x\]
和と差の微分
足し算や引き算の式を微分することもあります。
\(y=f(x)+g(x)\)を微分すると、
\[y^{\prime}=f^{\prime}(x)+g^{\prime}(x)\]
\(y=f(x)-g(x)\)を微分すると、
\[y^{\prime}=f^{\prime}(x)-g^{\prime}(x)\]
\(y=2{x}^{3}+x^{2}\)を微分しなさい。
この問題は\(2{x}^{3}\)と\(x^{2}\)をそれぞれ考えます。
\[y^\prime=6{x}^2+2x\]
定数の微分
\(x\)で微分するとき、\(x\)を持たない定数は微分すると0になってしまいます。
定数関数cを微分すると、
\[c^{\prime}=0\]
\(y=3{x}^{2}-4x+2\)を微分しなさい。
\(3{x}^{2}-4x\)はこれまで同様に微分すると、\(y=6x-4\)になることは分かりますね。残りの2は\(x\)を持たない定数なので0となります。
したがって、
\[y^{\prime}=6x-4\]
定数cを微分すると、なぜ0になるのかを説明します。
\(c\)を無理やり\(c x^{0}\)だと考えれば、微分したときに\(c \times 0\)なので0になります。
積の微分
\[{f(x)g(x)}^{\prime}=f^{\prime}(x)g(x)+f(x)g^{\prime}(x)\]
積の微分の公式はこのままだと覚えにくいと思います。そのため私は
(そのまま)(微分)+(微分)(そのまま)
と覚えています。
\(y=(x^{2}-3x-1)(x^{2}+4)\)を微分しなさい。
解答
\begin{eqnarray}
y^{\prime}&=&(x^{2}-3x-1)(x^{2}+4)\\
&=&(2x-3)(x^{2}+4)+(x^{2}-3x-1)\bullet 2x\\
&=&2x^{3}+8x-3x^{2}-12+2x^{3}-6x^{2}-2x\\
&=&4x^{3}-9x^{2}+6x-12
\end{eqnarray}
答え \(y^{\prime}=4x^{3}-9x^{2}+6x-12\)
商の微分
\[\displaystyle {\frac{f(x)}{g(x)}}^{\prime}=\frac{f^{\prime}(x)g(x)-f(x)g^{\prime}(x)}{g(x)^{2}}\]
積の微分の公式では足し算でしたが、商の微分の公式は分子が引き算になっていることに注意してください。
「分母は2乗、分子は積の微分の引き算バージョン」と考えると覚えやすいですね。
\(\displaystyle y=\frac{x^{2}-2}{2x+1}\)を微分しなさい。
\begin{eqnarray}
\displaystyle y^{\prime}&=&\frac{2x(2x+1)-(x^{2}-2x) \bullet 2}{(2x+1)^{2}}\\
\displaystyle &=& \frac{2(x^{2}-x-1)}{(2x+1)^{2}}
\end{eqnarray}
答え \frac{2(x^{2}+x+2)}{(2x+1)^{2}}
\(x^{n}\)の微分まとめ
今回は\(x^{n}\)の微分について解説していきました。
これは微分積分を学習してい上で絶対に欠かせない基本公式ですので、今回でマスターして定期テストに活かしましょう。
◎\(x^{n}\)の微分
\[(x^{n})^{\prime} =n x^{n-1}\]
◎定数倍の微分
\[y^{\prime}=k f^{\prime}(x)\]
◎和と差の微分
\(y=f(x)+g(x)\)を微分すると、
\[y^{\prime}=f^{\prime}(x)+g^{\prime}(x)\]
\(y=f(x)-g(x)\)を微分すると、
\[y^{\prime}=f^{\prime}(x)-g^{\prime}(x)\]
◎積の微分
\[{f(x)g(x)}^{\prime}=f^{\prime}(x)g(x)+f(x)g^{\prime}(x)\]
◎商の微分
\[\displaystyle {\frac{f(x)}{g(x)}}^{\prime}=\frac{f^{\prime}(x)g(x)-f(x)g^{\prime}(x)}{g(x)^{2}}\]
この計算はスムーズにできるようにしておきましょう。
ぜひ本サイトを活用して、微分への理解を深めてくださいね!
それでは最後までご覧いただきありがとうございました。
みんなの努力が報われますように!


コメント