数学Ⅱには微分積分があり、多くの高校生を悩ませる単元ですね。
今回解決する悩み
「平均変化率ってなに？」
「平均変化率の求め方が知りたい」
今回は微分法から平均変化率の意味や求め方を解説します。
高校生平均変化率の求め方がよく分からなくて…
“平均変化率”と聞いて、難しいイメージを持つ人も多いと思います。
しかし、意味が分かれば簡単で、中学校で習った変化の割合と同じです。
本記事では平均変化率の意味と求め方を解説します。
数学が苦手な方も平均変化率を求められるようになるので、ぜひ本記事を最後までご覧ください。
※本ページは学習アプリのプロモーションが含まれています。
シータ気になる見出しをクリックして、
ぜひ最後までご覧ください。
平均変化率とは？意味を確認
まずは前提として、平均変化率の意味から確認しておきましょう。
平均変化率の意味
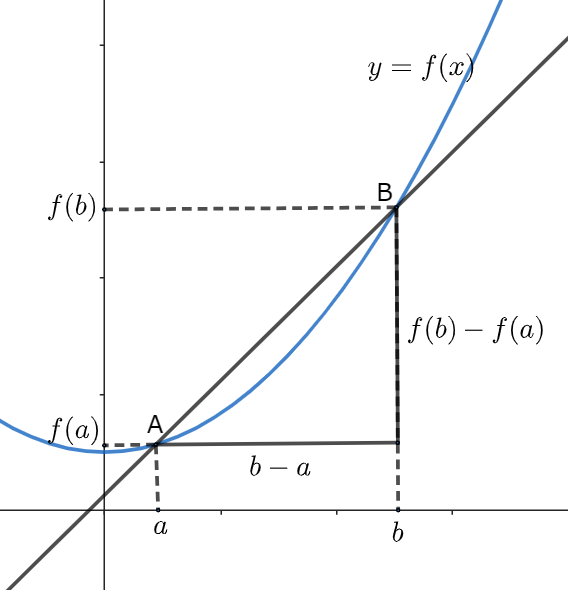
関数\(y=f(x)\)において、xの値がaからbまで変化するとき、
\[\displaystyle \frac{f(b)−f(a)}{b-a}\]
これを、\(y=f(x)\)におけるx=aからx=bまでの平均変化率という。
これだけ見てもよく分からないという人も多いのではないでしょうか。意味を理解すれば、そんなに難しいものではありません。
シータ公式を暗記するより意味を覚えた方が早いよ！
平均変化率は中学校で習った変化の割合と意味は同じです。
まず、変化の割合の復習からしていきましょう。
変化の割合とはxの値の変化に対して、yの値がどれだけ変化したかを表したものです。
式で書くと
\[変化の割合＝\displaystyle \frac{yの増加量}{xの増加量}\]
となります。
ちなみに、グラフで表すとこんな感じです。
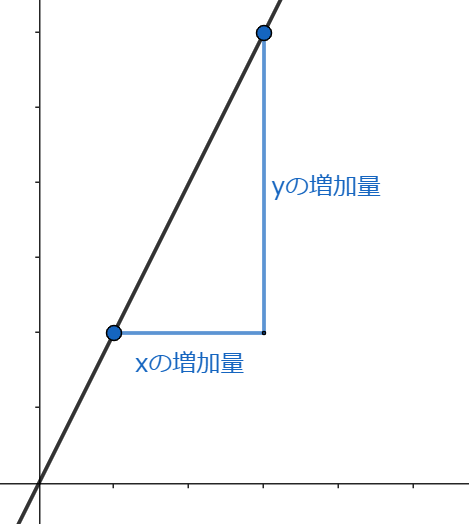
例として、\(y=2x\)のグラフを使って考えてみます。
xが0から2まで変化したとき変化の割合は
\[\frac{4−0}{2−0}＝2\]
となり、変化の割合は２となります。
平均変化率はこれと同じ考え方をすれば良いのです。
高校生中学でやったことと同じですね！
平均変化率の求め方
ここからは平均変化率の求め方について解説していきます。
先ほど、変化の割合の求め方を復習しましたが、平均変化率の求め方もそれと同じことをするだけです。
まず、平均変化率を求めるには先ほど紹介したこの公式を使います。
\[\displaystyle \frac{f(b)−f(a)}{b-a}\]
平均変化率を求める例題
例題
\(f(x)=2x^{2}−1\)において、\(x=0\)から\(x=2\)までの平均変化率を求めよ。
この例題を使って、平均変化率の求め方を解説していきます。
慣れるまでは図を書いてみるとイメージしやすくなると思います。
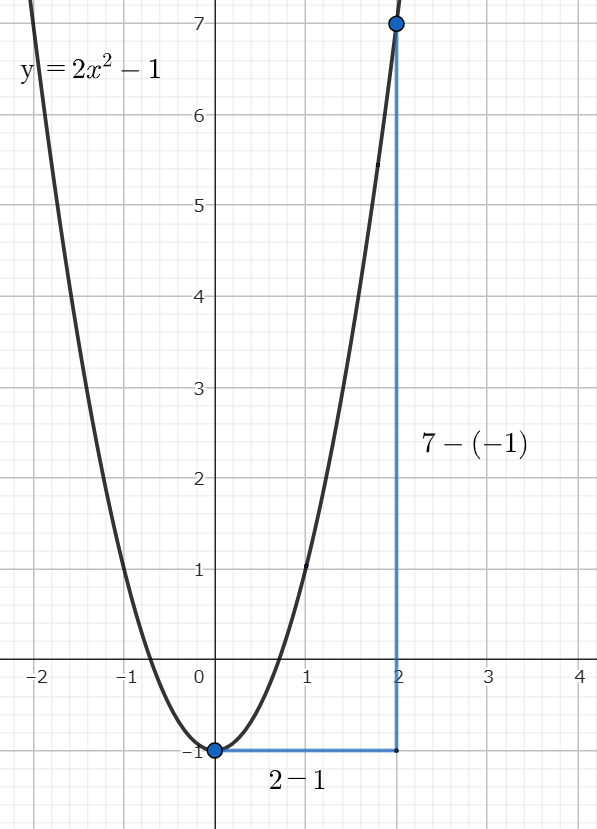
後は、公式に当てはめていくだけです。
\[\displaystyle \frac{f(2)-f(0)}{2-0}=\frac{7-(-1)}{2-0}=4\]
よって、平均変化率は4となります。
高校生ありがとうございます！だいぶ分かってきました！
平均変化率を求めよう！
では、実際に練習問題を解いて平均変化率を求めてみましょう！
練習問題
\(y=x^{2}\)において、\(x=1\)から\(x=3\)までの平均変化率を求めよう。
\(y=x^{2}\)において、\(x=1\)から\(x=1+h\)までの平均変化率を求めよう。
練習問題の解答
（１）
\begin{eqnarray}
\displaystyle \frac{f(3)−f(1)}{3−1}&=&\frac{3^2−1^2}{3−1}\\
&=&\frac{8}{2}\\
&=&4
\end{eqnarray}
答え 4
（２）
\begin{eqnarray}
\displaystyle \frac{f(1+ℎ)−f(1)}{(1+ℎ)−1}&=&\frac{(1+ℎ)^2−1^2}{(1+ℎ)−1}\\
&=&\frac{2ℎ+ℎ^2}{ℎ}\\
&=&\frac{ℎ(2+ℎ)}{ℎ}\\
&=&2+h
\end{eqnarray}
答え 2+ℎ
この問題は\(x=1+h\)を代入しなければならないので、少し計算がややこしくなるかもしれませんが、やり方は（１）と同じです。
平均変化率と微分係数の違い
微分法を学んでいると「微分係数」という言葉が出てきます。
「平均変化率」と「微分係数」の違いが分からない人もいるのではないかと思います。
微分係数の定義
まず、微分係数とは何か定義を説明します。
微分係数の定義
関数f(x)の\(x=a\)から\(x=a+h\)までの平均変化率
\[\displaystyle \frac{f(a+ℎ)−f(a)}{(a+h)-a}\]
において、hが０に限りなく近づくとき、その極限値を関数f(x)のx=aにおける微分係数または変化率という。
この定義では難しくて伝わらないと思うので、図を用いて説明していきます。
「平均の速度」と「瞬間の速度」
皆さんは「平均の速度」「瞬間の速度」という言葉を聞いたことがありますか。
この「平均の速度＆瞬間の速度」と「平均変化率＆微分係数」を結びつけて考えていきます。
よく分からなくても説明を読んでもらえれば納得できると思うので、ここはじっくりと呼んでください。
まず、2000ｍの距離を10分で走ったとします。この時の走る速さは分速200mとすぐに計算できますね。
これが平均の速度、つまり平均変化率です。
ですが、実際に走る場合、2000ｍをずっと一定の速さで走るわけではありませんよね。
下の図のように2000ｍを走るとき分速200mよりも速くなったり、遅くなったりします。
これが瞬間の速度であり、微分係数の意味です。
先ほどの例で考えると平均変化率を求める時、分母は時間でしたよね。この時間の間隔を10分ではなく、1秒、0.1秒とどんどん狭くしていく、つまり限りなく0に近づけると正確な瞬間の速度を求めることができます。
今回は速度を例に考えましたが、ある1点における速度みたいなものを微分係数といいます。
平均変化率と微分係数の違い
次に平均変化率と微分係数の違いを傾きに着目して説明していきます。
ポイント
・平均変化率
→ある2点を通る直線の傾き
・微分係数
→グラフ上の接点における接線の傾き
これをグラフで考えるとすぐに分かると思います。
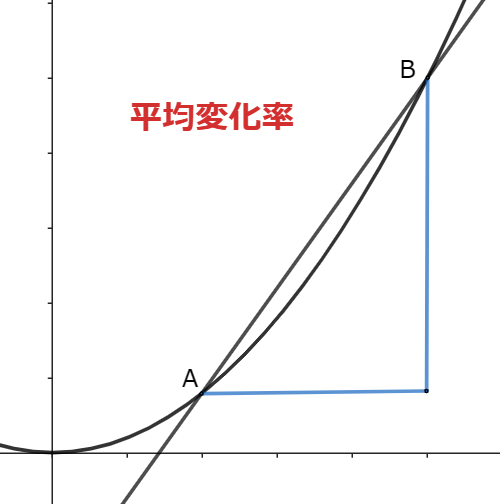
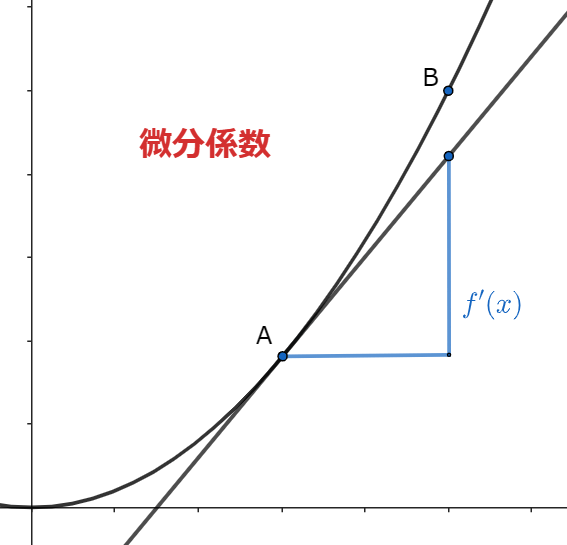
この図で考えると、平均変化率は直線ABの傾きになっていることが分かります。
また、微分係数は点Aにおける接線の傾きになっています。
つまり、この図で言うと「平均変化率を求めよ」と「直線ABの傾きを求めよ」は同じ意味であり、「微分係数を求めよ」と「点Aにおける接線の傾きを求めよ」は同じ意味であるといえます。
平均変化率の意味と求め方 まとめ
今回は微分法から平均変化率の意味と求め方を解説しました。
平均変化率という名前から、難しく考えてしましがちですが意外と簡単に求められることが分かったと思います。
平均変化率の求め方平均変化率とはxの値の変化に対して、yの値がどれだけ変化したかを表したものです。
平均変化率の意味
関数\(y=f(x)\)において、xの値がaからbまで変化するとき、
\[\displaystyle \frac{f(b)−f(a)}{b-a}\]
これを、\(y=f(x)\)におけるx=aからx=bまでの平均変化率という。
この公式は頑張って覚えようとしなくても、平均変化率の意味さえしっかり理解していればすぐにわかるようになります。
また、平均変化率と微分係数の違いもしっかりおさえて、問題で何を求めればよいのかが分かるようにしておきましょう！
ぜひこの記事で紹介した考え方を参考にしてみてください！
コメント