3乗の展開をします。展開したい式のタイプを選択し、係数の入力後、算出ボタンをクリックしてください。
を展開すると、になります。
a の値は0以外を入力してください。
 高校生
高校生計算に困っていたので助かりました!
今回は3乗の展開公式に関する悩みを解決します。
「3乗の計算が苦手」
「3乗の展開公式が覚えられない」
こんな悩みを解決する記事を書いていきます。
\((x+3)^3\)
こんな問題よく見ますよね。
今回はこの問題を解けるようにしていきましょう!
 高校生
高校生毎回展開するのが結構大変なんですよ
3乗の展開公式が使いこなせれば、計算もスムーズになります!
三乗の展開公式
\((a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}\)
\((a-b)^{3}=a^{3}-3a^{2}b+3ab^{2}-b^{3}\)
(a±b)3乗の展開は上記のような式になります。
少し複雑に見えますが、3乗の展開公式は覚えてしまうのが良いでしょう
(a±b)3乗の展開公式 証明
\((a±b)^{3}\)の展開公式を証明していきましょう。
証明は計算していくだけなのでかなりシンプルです。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
・\((a+b)^{3}\)の証明
\begin{eqnarray}
(a+b)^{3}&=&(a+b)^{2}(a+b)\\
&=&(a^{2}+2ab+b^{2})(a+b)\\
&=&a^{3}+3a^{2}b+3ab^{2}+b^{3}\\
\end{eqnarray}
・\((a+b)^{3}\)の証明
\begin{eqnarray}
(a-b)^{3}&=&(a-b)^{2}(a-b)\\
&=&(a^{2}-2ab+b^{2})(a-b)\\
&=&a^{3}-3a^{2}b+3ab^{2}-b^{3}\\
\end{eqnarray}
[/st-mybox]
どちらも中学で習う展開公式を用いて、少しずつ展開していくことで証明ができました。
(a+b)3乗の公式使ってみる
では、冒頭の課題問題を実際に解いてみましょう。
\((x+3)^3\)
3乗の展開公式に代入しながら計算していきましょう。
\((a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}\)
\((a-b)^{3}=a^{3}-3a^{2}b+3ab^{2}-b^{3}\)
\((x+3)^{3}\)
\(=x^{3}+3x^{2}\times{3}+3x\times{3^{2}}+3^{3}\)
\(=x^{3}+9x^{2}+27x+27\)
公式を覚えていると計算がかなり早くなります。
 高校生
高校生でも公式が覚えられなくて…
 シータ
シータ次は3乗の展開公式の覚え方を紹介するよ!
3乗の展開公式 覚え方
それでは3乗の展開公式の覚え方を紹介します。
合言葉は
3と21・12
です!
何のことかというと
3乗の展開公式はすべての項に3が入っています。
初めと終わりの項が3乗されるのは覚えやすいと思います。
覚えづらいのが中央の2項です。
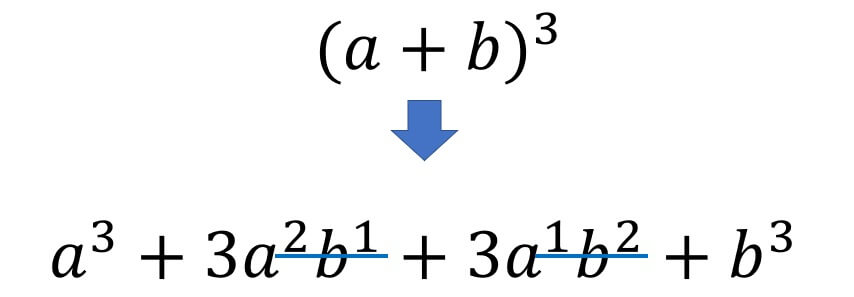
中央の2項に関しては、2乗1乗・1乗2乗となるように掛け合わせたものを3倍すれば展開は終了です。
合言葉は
「3と21・12」
3乗の展開公式<練習問題>

では練習問題を解いて慣れていきましょう。
\((x+2)^{3}\)
それでは3乗の展開公式に当てはめてみましょう。
合言葉は「3と21・12」
\((x+2)^{3}\)
\(=x^{3}+3・x^{2}・2+3・x・2^{2}+2^{3}\)
\(=x^{3}+6x^{2}+12x+8\)
複雑な計算なので、計算ミスに気を付けてください。
計算ミスをすると公式を覚えた意味も無くなります。
\((x-3)^{3}\)
次は符号がマイナスの問題です!
\((a-b)^3=a^{3}-3a^{2}b+3ab^{2}-b^{3}\)
この公式を使っていきましょう!
\((x-3)^{3}\)
\(=x^{3}-3・x^{2}・3+3・x・3^{2}-3^{3}\)
\(=x^{3}-9x^{2}+27x-27\)
\((3x+2)^{3}\)
最後は先頭の項に係数がある問題です。
これも公式に従って代入するだけです。
\((3x+2)^{3}\)\(=(3x)^{3}+3・(3x)^{2}・2+3・(3x)・2^{2}+2^{3}\)
\(=27x^{3}+54x^{2}+36x+8\)
問題なく解くことができました!
\((a±b)^{3}\)の展開公式 まとめ
今回は数学Ⅱの3乗の展開公式と覚え方についてまとめました。
[st-mybox title=”ポイント” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\((a±b)^{3}\)の展開公式
\((a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}\)
\((a-b)^{3}=a^{3}-3a^{2}b+3ab^{2}-b^{3}\)
3乗の展開公式の覚え方
「3と2乗1乗・1乗2乗」
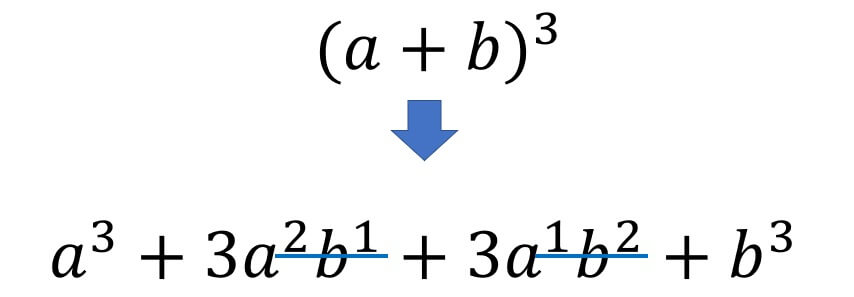
[/st-mybox]
教科書に内容に沿って解説記事を載せていきます。
お気に入り登録して定期試験前の確認に活用してください。
では、ここまで読んでくださってありがとうございました。
みんなの努力が報われますように!

