今回解決する悩み
「因数分解が苦手…」
「たすき掛けのやり方を知りたい」
今回は数学Ⅰの「数と式」からこんな悩みを解決します。
 高校生
高校生たすき掛けを使った因数分解のやり方を教えて欲しいです。
因数分解の公式ってややこしいですよね。
本記事ではたすき掛けを使った因数分解のやり方を解説します。
目次
たすき掛けの因数分解
\(3x^2+14x+8=(x+4)(3x+2)\)
この方程式をたすき掛けで因数分解しましょう。
\(x^2\)の係数と一番後ろの定数項に注目します。
今回ならば、\(x^2\)の係数が3、定数項が8です。
次に、積が3になる数の組と積が8になる数の組を考えます。
掛けて3になる組は、
{1,3}、{-1,3}
掛けて8になる組は
{1,8}、{2,4}、{-1,-8}、{-2,-8}
あとはステップの従っていくだけです。

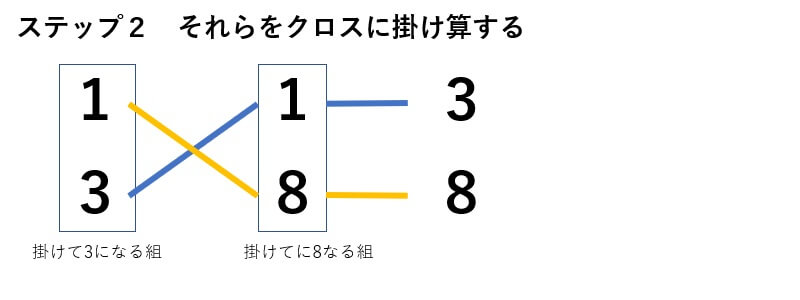
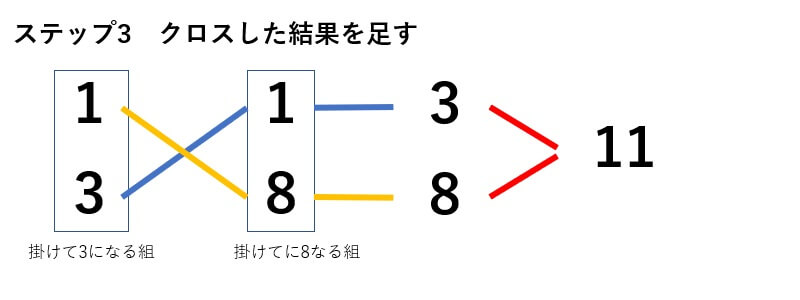
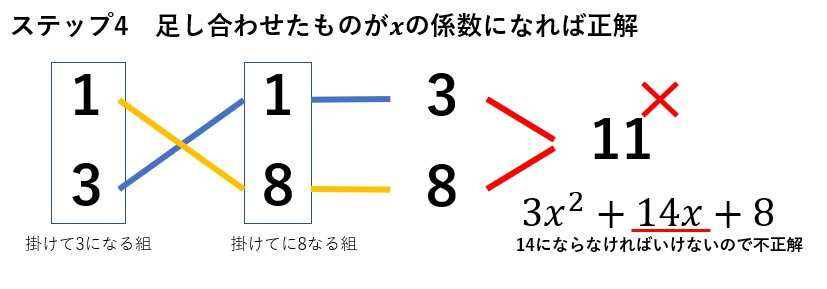
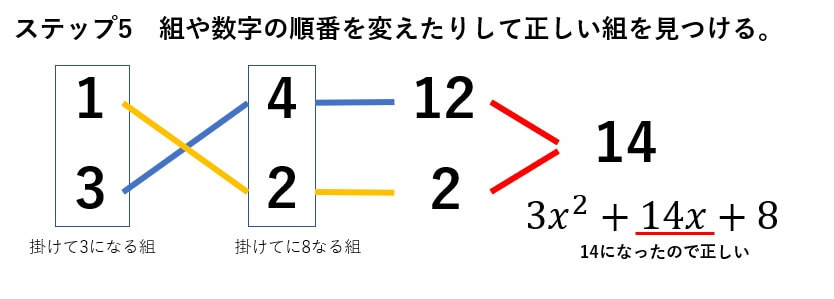
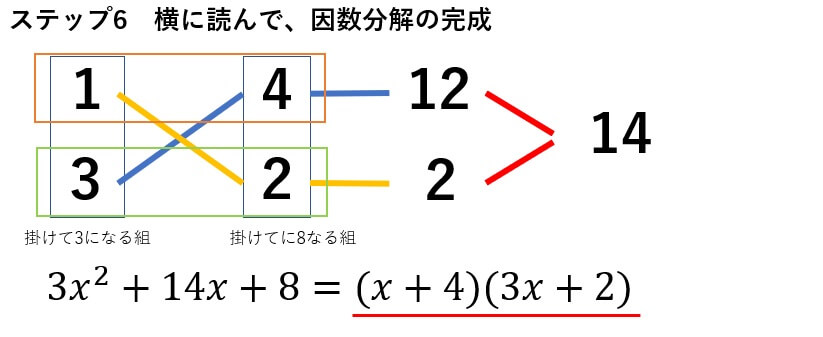
先ほども言ったように慣れてくると、直感で数字の組が分かるようになってきます。
それまではたすき掛けで経験値を積んでいきましょう。
では、練習問題です。

因数分解の工夫
最後にちょっとした応用です。
こんな問題はどうでしょう。
次の式を因数分解せよ。
\((x+y)^2+2(x+y)-8\)
\((x+y)^2+2(x+y)-8\)
中学校ではこの類の問題を解くときは
\((x+y)\)の部分を\(A\)と置き換えて解きましたが、高校生になったのでそのステップは飛ばしましょう。
\((x+y)^2+2(x+y)-8\)
\(=\{(x+y)+4\}\{(x+y)-2\}\)
\(=(x+y+4)(x+y-2)\)
\(=\{(x+y)+4\}\{(x+y)-2\}\)
\(=(x+y+4)(x+y-2)\)
このようにスマートに解けるようになりたいですね!
練習問題をつけておきます。

たすき掛けの因数分解 おわりに
今回はたすき掛けを使って因数分解する方法ついてまとめました。






では、ここまで読んでくださってありがとうございました。
みんなの努力が報われますように!


コメント