「2点の距離を求めたい」
「2点間の距離を求める公式を忘れた」
今回はこんな悩みを解決していきましょう。
 高校生
高校生距離を求めたいんだけど公式を忘れちゃって…
平面における2点間の距離は以下の公式で求めることができます。
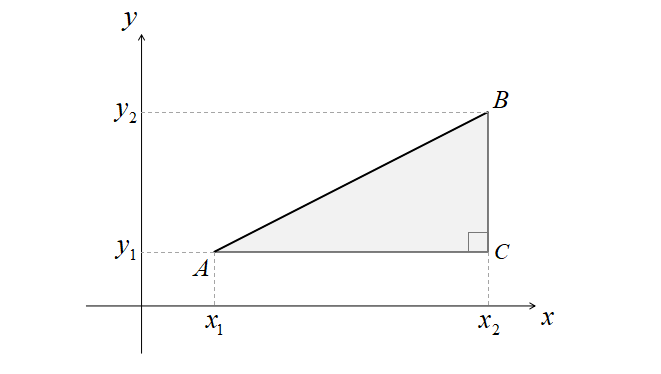
[st-mybox title=”2点間の距離の公式” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
2点\(A\left(x_{1},y_{1}\right)\),\(B\left(x_{2},y_{2}\right)\)間の距離\(AB\)は
\[AB=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\]
[/st-mybox]
決して難しい公式ではないので、使いこなせるようになりたい公式です。
本記事では2点間の距離の公式について解説しました。
平面だけでなく、空間上の2点間の距離についても解説しているので、ぜひ最後までご覧ください。
 シータ
シータ気になる見出しをクリックして、
ぜひ最後までご覧ください。
[st_af id=”13737″]
2点間の距離とは?
2点間の距離とは、2点\(A,B\)があるときの線分\(AB\)の長さを指します。
距離とは最短経路なので、曲線ではなく直線でつないでください。
2点間の距離の公式
2点間の距離は以下の公式で求めることができます。
[st-mybox title=”2点間の距離の公式” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
2点\(A\left(x_{1},y_{1}\right)\),\(B\left(x_{2},y_{2}\right)\)間の距離\(AB\)は
\[AB=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\]
[/st-mybox]
具体例をもとに2点間の距離を考えてみましょう。
2点\(A\left(1,2\right)\),\(B\left(5,5\right)\)があるとき、その距離\(AB\)は
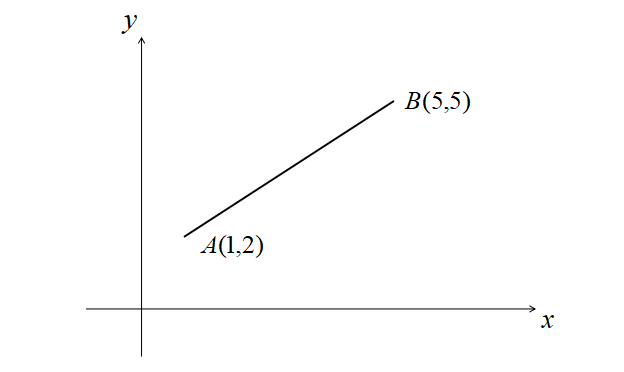
\begin{eqnarray}
AB&=&\sqrt{\left(5-1\right)^{2}+\left(5-2\right)^{2}}\\
&=&\sqrt{4^{2}+3^{2}}\\
&=&\sqrt{25}\\
&=&5
\end{eqnarray}
これで2点\(A,B\)間の距離を求めることができました。
距離の公式の証明
なぜ2点間の距離の公式が成り立つのか考えてみましょう。
どの公式でも公式の仕組みを理解しておくと覚えやすいです。
2点\(A\left(x_{1},y_{1}\right)\),\(B\left(x_{2},y_{2}\right)\)とすると、下の図の直角三角形ABCを描くことができます。
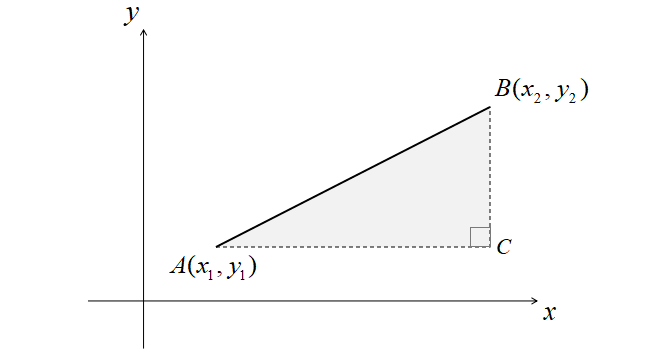
三平方の定理より
\[AB^{2}=AC^{2}+BC^{2}\]
が成り立つので
\[AB^{2}=\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}\]
となります。
したがって、
\[AB=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\]
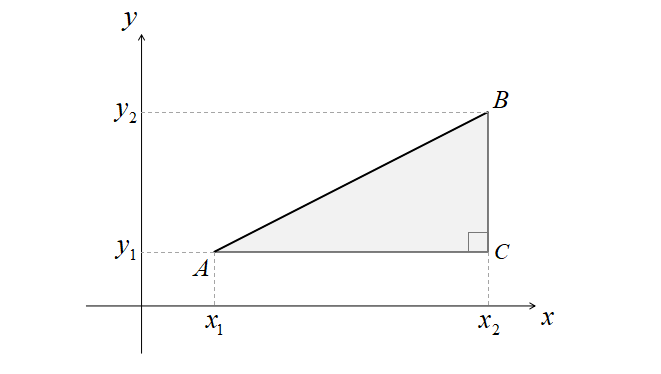
 高校生
高校生中学校で習った三平方の定理を活用しているんですね!
3次元における2点間の距離
ここまでは\(xy\)平面の2次元における距離\(AB\)を考えてきました。
次は3次元における2点間の距離を求めてみましょう。
[st-mybox title=”空間上の2点間の距離の公式” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
2点\(A\left(x_{1},y_{1},z_{1}\right)\),\(B\left(x_{2},y_{2},z_{2}\right)\)間の距離\(AB\)は
\[AB=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}\]
[/st-mybox]
空間上の2点\(A\left(1,2,2\right)\),\(B\left(4,5,5\right)\)間の距離\(AB\)は
\begin{eqnarray}
AB&=&\sqrt{\left(4-1\right)^{2}+\left(5-2\right)^{2}+\left(5-2\right)^{2}}\\
&=&\sqrt{3^{2}+3^{2}+3^{2}}\\
&=&\sqrt{27}\\
&=&3\sqrt{3}
\end{eqnarray}
3次元になると座標が1つ増えましたね。
しかし、3次元でも公式の使い方は2次元と変わらないので簡単です。
 シータ
シータ3次元の距離も求められるようにしておこう!
原点からの距離
原点からの距離を求めることもできます。
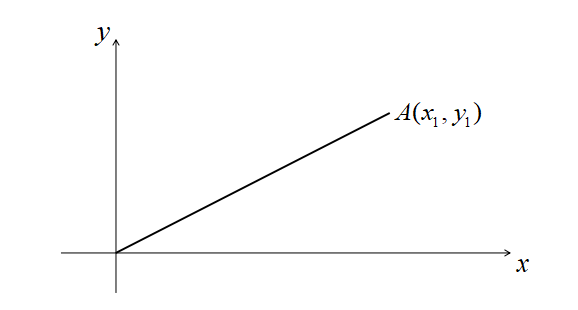
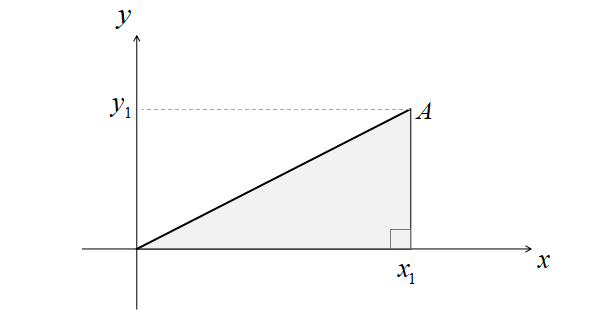
原点を\(O\left(0,0\right)\)と考えて、点\(A\left(x_{1},y_{1}\right)\)との距離\(OA\)は
\[OA=\sqrt{x_{1}^{2}+y_{1}^{2}}\]
2点間の距離の証明と同様に、三平方の定理を考えれば納得できると思います。
 高校生
高校生これは簡単ですね!
 シータ
シータそうだね!2点間の距離の公式に(0,0)を代入すれば自然と求められるよ
2点間の距離を求める《練習問題》

2点間の距離の公式を用いて練習問題にチャレンジしてみよう!
[st-mybox title=”練習問題” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
次の2点間の距離を求めてみよう。
(1) \(A\left(1,2\right),B\left(4,6\right)\)
(2) \(A\left(-3,1\right),B\left(2,-4\right)\)
(3) 原点\(O\),\(A\left(2,3\right)\)
[/st-mybox]
 シータ
シータ公式に代入するだけなので難しくないね!
練習問題(1)の解説
2点\(A\left(1,2\right),B\left(4,6\right)\)の座標が分かっているので、2点間の距離の公式に代入して
\begin{eqnarray}
AB&=&\sqrt{\left(4-1\right)^{2}+\left(6-2\right)^{2}}\\
&=&\sqrt{9+16}\\
&=&\sqrt{25}\\
&=&5
\end{eqnarray}
したがって、2点\(AB\)の距離は5だと分かりました。
練習問題(2)の解説
練習問題(2)も(1)と同様に
\begin{eqnarray}
AB&=&\sqrt{\left(2-(-3)\right)^{2}+\left(-4-1\right)^{2}}\\
&=&\sqrt{25+25}\\
&=&\sqrt{50}\\
&=&5\sqrt{2}
\end{eqnarray}
したがって、2点\(AB\)の距離は\(5\sqrt{5}\)
練習問題(3)の解説
原点\(O\)と\(A\left(2,3\right)\)の距離なので、
\begin{eqnarray}
OA&=&\sqrt{2^{2}+3^{2}}\\
&=&\sqrt{13}
\end{eqnarray}
したがって、
\[OA=\sqrt{13}\]
 高校生
高校生自分の力で解くことができました!
2点間の距離の公式 まとめ
今回は2点間の距離の公式についてまとめました。
[st-marumozi fontawesome=”” bgcolor=”#FFB74D” bordercolor=”” color=”#fff” radius=”30″ margin=”0 10px 10px 0″ myclass=””]2点間の距離の公式 まとめ[/st-marumozi]
2点間の距離を求める公式があります。
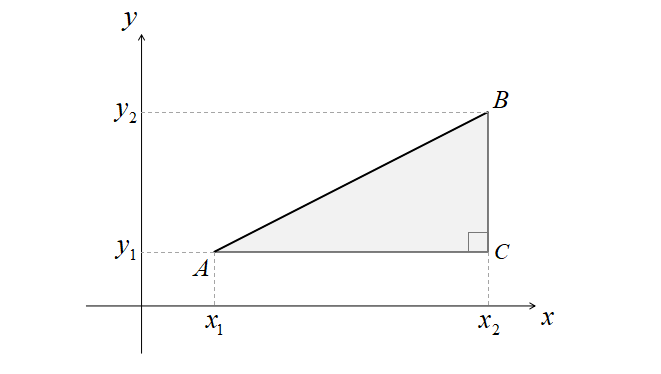
[st-mybox title=”2点間の距離の公式” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
2点\(A\left(x_{1},y_{1}\right)\),\(B\left(x_{2},y_{2}\right)\)間の距離\(AB\)は
\[AB=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\]
[/st-mybox]
3次元における2点間の距離は以下の公式で求められます。
[st-mybox title=”空間上の2点間の距離の公式” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
2点\(A\left(x_{1},y_{1},z_{1}\right)\),\(B\left(x_{2},y_{2},z_{2}\right)\)間の距離\(AB\)は
\[AB=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}\]
[/st-mybox]
数Ⅱの図形と方程式には重要な公式がたくさん出てきます。
内分点や外分点もスムーズに求められるようにしておきましょう。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
[/st-mybox]



コメント