[mathjax]
[st-mybox title=”今回解決する悩み” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”4″ borderradius=8″ titleweight=”bold” fontsize=”110″ myclass=”nayami-box” margin=””]
「等しいベクトルとは?」
「ベクトルの大きさって?」
[/st-mybox]
ベクトルの”大きさ”とは長さを表しています。
大きさの求め方は簡単なので必ず押さえておきましょう。
本記事では、ベクトルの大きさを求める公式を解説しています。
ベクトルの大きさと求め方
下図のような大きさと向きで定まるものをベクトルといいます。
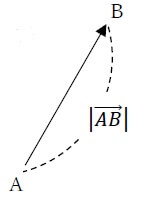
有向線分ABで表されるベクトルを、\(\overrightarrow{ AB }\)と書き表す。
このとき、線分ABの長さをベクトルABの“大きさ”として\(|\overrightarrow{ AB }|\)と表します。
平面ベクトルのとき
平面ベクトルの大きさの求め方を紹介します。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(\vec{AB} = (x, y)\)の大きさ\(|\overrightarrow{ AB }|\)は、
\[|\overrightarrow{ AB }|=\sqrt{x^2 + y^2}\]
[/st-mybox]
\(A(0,0),B(3,4)\)とすると\(\vec{AB} = (3, 4)\)の大きさは、
\[|\overrightarrow{ AB }|=\sqrt{3^2 + 4^2}=\sqrt{25}=5\]
したがって、\(\vec{AB} = (3, 4)\)の大きさは5ということが分かりました。
空間ベクトルのとき
空間ベクトルの場合は成分が3つになるので、大きさの求め方も変わります。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(\vec{AB} = (x, y, z)\)の大きさ\(|\overrightarrow{ AB }|\)は、
\[|\overrightarrow{ AB }|=\sqrt{x^2 + y^2 +z^2}\]
[/st-mybox]
\(A(0,0,0),B(3,4,5)\)とすると\(\vec{AB} = (3, 4,5)\)の大きさは、
\[|\overrightarrow{ AB }|=\sqrt{3^2 + 4^2 +5^2}=\sqrt{50}=5\sqrt{2}\]
したがって、\(\vec{AB} = (3, 4 ,5)\)の大きさは\(5\sqrt{2}\)ということが分かりました。
単位ベクトルは大きさ1
単位ベクトルとは、大きさが1のベクトルです。
単位ベクトルの具体例を見てみましょう。
\(\displaystyle A(0,0),B(\frac{3}{5},\frac{4}{5})\)とすると\(\displaystyle \vec{AB} = (\frac{3}{5}, \frac{4}{5})\)です。
このとき\(\displaystyle \vec{AB} = (\frac{3}{5}, \frac{4}{5})\)の大きさは、
\[\displaystyle |\overrightarrow{ AB }|=\sqrt{(\frac{3}{5})^2 + (\frac{4}{5})^2}=\sqrt{\frac{9}{25} + \frac{16}{25}}=1\]
したがって、\(\displaystyle \vec{AB} = (\frac{3}{5}, \frac{4}{5})\)は大きさが1なので単位ベクトルです。
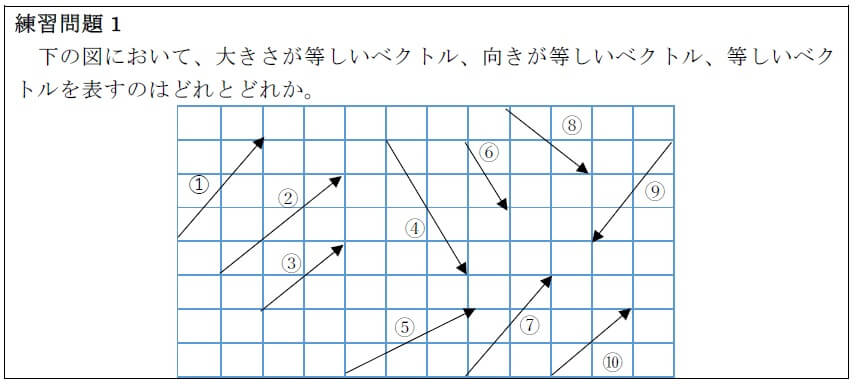
大きさの等しいベクトルとは?
\(\vec{a}と\vec{b}\)の向きと大きさが等しいとき、
2つのベクトルは等しいといい、\(\vec{a}=\vec{b}\)と書く。
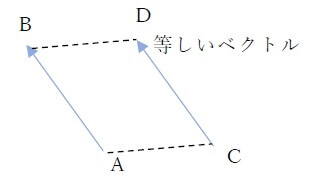
大きさも向きも等しいので、等しい2つのベクトルは平行移動するとぴったりと重ねることができます。
なぜベクトルの大きさは2乗?
ベクトルの大きさは先に2乗して、あとから2乗を外す求め方もあります。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(A(0,0),B(3,4)\)とすると
\[|\overrightarrow{ AB }|^{2}=3^2 + 4^2=25\]
\(|\overrightarrow{ AB }| \ge 0\)なので、
\[|\overrightarrow{ AB }|=5\]
[/st-mybox]
 シータ
シータ新しい公式に見えるけどさっきと同じだよ
先ほど解説した公式では、ルートを使いましたがこの公式ではルートを後回しにできます。
ベクトルの大きさ まとめ
今回はベクトルの大きさについてまとめました。
[st-marumozi fontawesome=”” bgcolor=”#FFB74D” bordercolor=”” color=”#fff” radius=”30″ margin=”0 10px 0 0″ myclass=””]ベクトル大きさ[/st-marumozi]
平面ベクトルの大きさの求め方
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(\vec{AB} = (x, y)\)の大きさ\(|\overrightarrow{ AB }|\)は、
\[|\overrightarrow{ AB }|=\sqrt{x^2 + y^2}\]
[/st-mybox]
空間ベクトルの大きさの求め方
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(\vec{AB} = (x, y, z)\)の大きさ\(|\overrightarrow{ AB }|\)は、
\[|\overrightarrow{ AB }|=\sqrt{x^2 + y^2 +z^2}\]
[/st-mybox]
ベクトルが苦手な方は多いと思いますが、慣れるまでは矢印だと思えば良いです。
まずは公式をしっかりと覚えてからが勝負です。
教科書に内容に沿った解説記事を挙げているので、定期試験前に確認してください。
それでは最後までご覧いただきありがとうございました。
みんなの努力が報われますように!

