[st-mybox title=”今回解決する悩み” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”4″ borderradius=8″ titleweight=”bold” fontsize=”110″ myclass=”nayami-box” margin=”40px auto 30px”]
「ベクトルのなす角ってなに?」
「角度をどうやって求めるの?」
[/st-mybox]
今回は数学Bのベクトルから「ベクトルのなす角」に関するこんな悩みを解決します。
 高校生
高校生ベクトルを習い始めたばかりで…
2つのベクトルがあるとき、2ベクトルの間には角が生まれます。この角のことを“なす角”と呼びます。
[st-mybox title=”ベクトルのなす角” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#fafafa” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
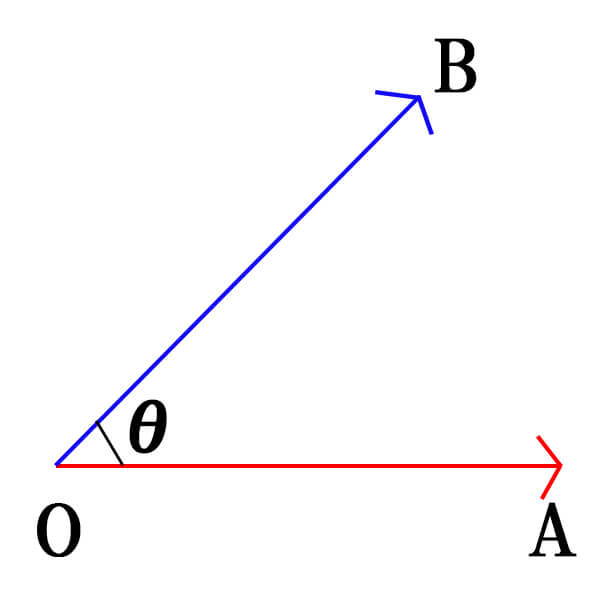
ベクトルのなす角とは、2つのベクトルの始点同士を重ねた場合に作られる\(180^\circ\)以下の角度のこと。
[/st-mybox]
なす角は180度を超えないのもポイントです。
本記事では「ベクトルのなす角」を練習問題も交えながら解説していきます。
平面ベクトルの場合と、空間ベクトルの場合どちらもしっかりマスターしていきましょう!
 シータ
シータベクトルが苦手な方は
ぜひ最後までご覧ください。
それではベクトルのなす角について解説していきましょう。
[st_af id=”13737″]
ベクトルのなす角とはどこ?
そもそも、ベクトルのなす角とはどの角のことでしょうか?
実は、ベクトルのなす角については以下のように考えるルールがあります。

[st-midasibox title=”ベクトルのなす角” fontawesome=”fa-check-circle faa-ring animated” bordercolor=”#FFC107″ color=”” bgcolor=”#FFFDE7″ borderwidth=”” borderradius=”5″ titleweight=”bold” myclass=””]
2つのベクトルの始点同士を重ねた場合に作られる\(180^\circ\)以下の角度のこと。
[/st-midasibox]
必ず180度より小さい方の角を“なす角”とします。
また、2つのベクトルの「始点」についても考え方があります。
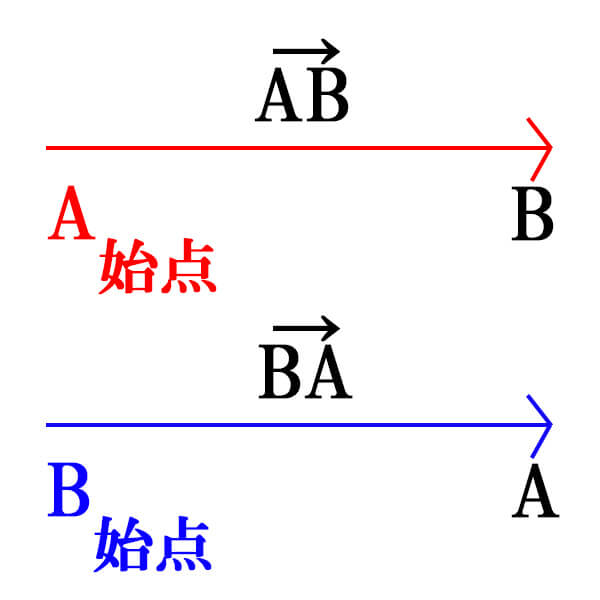
始点とは、\(\vec{AB}\)だったら点A、\(\vec{BA}\)だったら点Bのように、ベクトルの左側の文字で表される点のことを指します。
先ほど述べたように、ベクルのなす角は2つのベクトルの始点同士を重ねて求めるものでした。
ですので、下図のように始点が重なっていない場合は、平行移動して始点同士を重ねる必要があります。
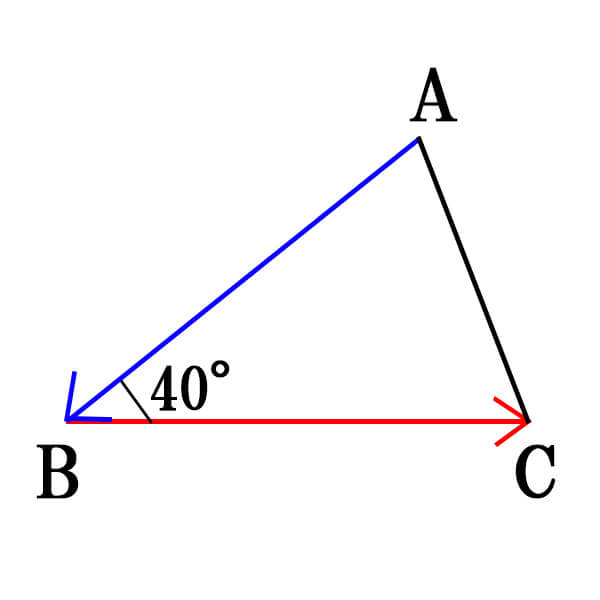
上の図を見てください。
この場合、\(\vec{AB}\)と\(\vec{BC}\)のなす角は何度になるでしょうか?
パッと見ただけだと「\(40^\circ\)」と答えそうになりますが、\(\vec{AB}\)と\(\vec{BC}\)は、始点同士が重なっていないため、このままでは求めることができません。
ベクトルを平行移動して、始点同士を重ねてみましょう。
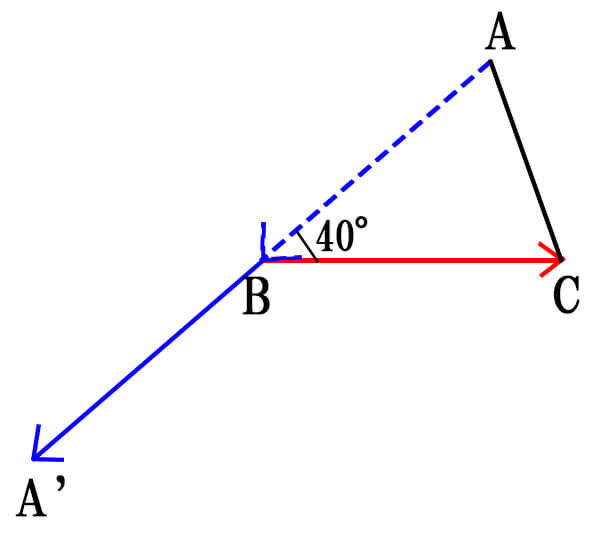
\(\vec{AB}\)を平行移動し、始点同士を重ねると上のような図になることが分かりました。
よって、\(\vec{AB}\)と\(\vec{BC}\)のなす角は、\(\vec{BA’}\)と\(\vec{BC}\)のなす角になることが分かりました。
ですので、答えは\(180^\circ – 40^\circ=140^\circ\)となります。
[st-midasibox-intitle title=”この見出しのまとめ” fontawesome=”fa-check-circle” bordercolor=”#03A9F4″ color=”#fff” bgcolor=”#E1F5FE” borderwidth=”” borderradius=”5″ titleweight=”bold” myclass=””]
- ベクトルのなす角とは、2つのベクトルの始点同士を重ねた場合に作られる\(180^\circ\)以下の角度のこと。
- 2ベクトルの始点が重なっていない場合は、一方のベクトルを平行移動して始点を重ねる必要がある。
[/st-midasibox-intitle]
ベクトルのなす角を求める
では、ベクトルのなす角について分かったところで、ベクトルのなす角の大きさを求めてみましょう。
平面ベクトルの場合
[st-mybox title=”例題①” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
2つのベクトル\(\vec{AB}\),\(\vec{BC}\)のなす角を求めてみましょう。
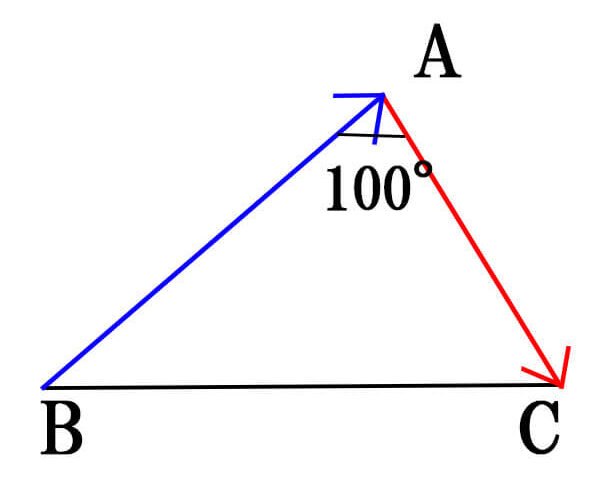
[/st-mybox]
この場合は、2つのベクトルの始点が重なっていないため、\(\vec{AB}\)を平行移動して2つのベクトルの始点を重ねます。
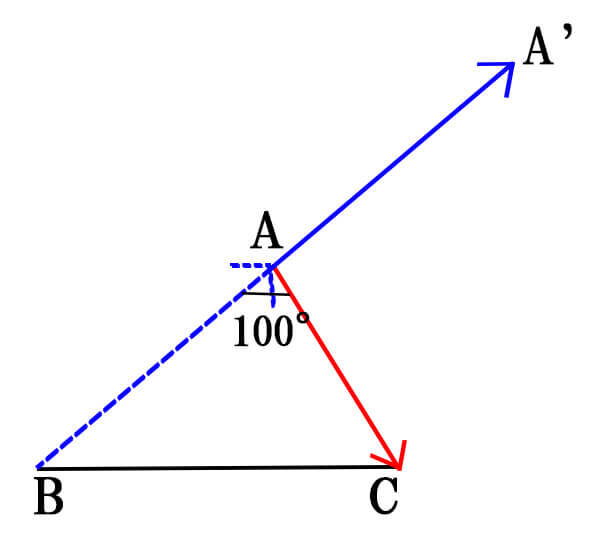
上の図より、\(\vec{AB}\),\(\vec{BC}\)のなす角は、\(\vec{BC}\)と\(\vec{BA’}\)となることが分かりました。
よって、答えは\(180^\circ-100^\circ=80^\circ\)
[st-mybox title=”例題②” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
2つのベクトル\(\vec{a},\vec{b}\)のなす角を求めてみましょう。
\(|\vec{a}|=\sqrt3,|\vec{b}|=2,\vec{a} \cdot \vec{b}=2\)
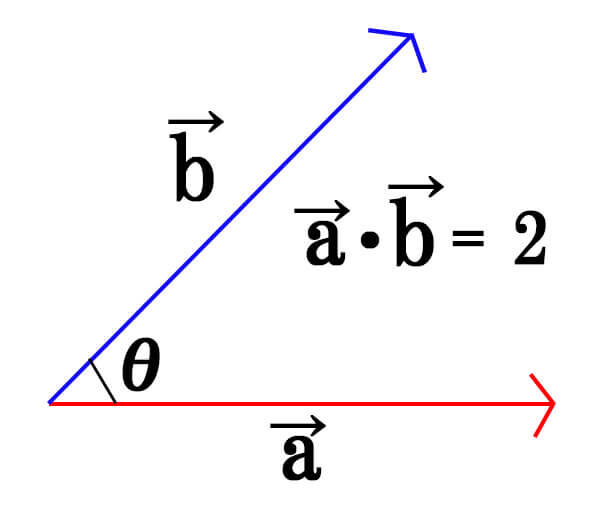
[/st-mybox]
この場合はベクトル\(\vec{a},\vec{b}\)の始点は重なっているため、平行移動は必要ありません。
問題で与えられた情報を使って、\(\vec{a},\vec{b}\)のなす角\(\theta\)を求めます。
問題では、2つのベクトルの大きさと内積が与えられていますね。
ここで内積の定義について復習してみましょう。
\(\vec{a},\vec{b}\)のなす角を\(\theta\)とすると、
\[\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}|\cos{\theta}\]
ここに、問題で与えられた数値を当てはめると
\begin{eqnarray}
2&=&\sqrt3 \cdot 2 \cdot \cos{\theta}\\
\cos{\theta}&=&\frac{1}{\sqrt3}
\end{eqnarray}
よって、\(\vec{a},\vec{b}\)のなす角は\(\theta=60^\circ\)となる。
空間ベクトルの場合
空間ベクトルの場合も、考え方は平面ベクトルの時と同様です。
ただ、空間ベクトルのなす角を求める問題は、内積を使って求める問題が多いですので、そちらを例題として解いてみましょう。
[st-mybox title=”例題③” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(\vec{a}=(1,2,-3), \vec{b}=(2,-3,1)\)であるとき、\(\vec{a},\vec{b}\)のなす角\(\theta\)を求めてみましょう。
[/st-mybox]
ここでは、\(\vec{a},\vec{b}\)の成分表示が与えられています。
内積を使いながら、\(\vec{a},\vec{b}\)のなす角\(\theta\)を求められそうです。
問題で与えられている数字から、分かるものを計算してみましょう。
\begin{eqnarray}
|\vec{a}|&=&\sqrt{1^2+2^2+{(-3)}^2}=\sqrt{14}\\
|\vec{b}|&=&\sqrt{2^2+{(-3)}^2+1^2}=\sqrt{14}\\
\vec{a} \cdot \vec{b}&=&1\times2+2 \times (-3) \times (-3) \times 1=-7
\end{eqnarray}
\(\vec{a} \cdot \vec{b} =|\vec{a}||\vec{b}|\cos{\theta}\)より
\begin{eqnarray}
-7&=&\sqrt{14}\times\sqrt{14}\times\cos{\theta}\\
\cos{\theta}&=&-\frac{1}{2}
\end{eqnarray}
よって、\(\theta=120°\)
角度を求めよう《練習問題》
なす角の求め方も分かったところで、いくつか練習問題に挑戦しましょう!
[st-mybox title=”練習問題①” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(\vec{a}=(-2,1),\vec{b}=(6,-3)\)であるとき、\(\vec{a},\vec{b}\)のなす角\(\theta\)を求めてみましょう。
[/st-mybox]
解答をチェックする
\(|\vec{a}|=\sqrt{{(-2)}^2+1^2}=\sqrt5\)
\(|\vec{b}|=\sqrt{6^2+{(-3)}^2}=\sqrt{45}=3\sqrt5\)
また、\(\vec{a},\vec{b}\)の内積\(\vec{a} \cdot \vec{b}\)は、
\[\vec{a} \cdot \vec{b}=(-2) \times 6+1 \times (-3)=-15\]
\(\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}|\cos{\theta}\)より、
\[-15=\sqrt5\times3\sqrt5\times\cos{\theta}\]
ゆえに、\[\cos{\theta=-1}\]
よって、\(\theta=180°\)
[st-mybox title=”練習問題②” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\(\vec{a}=(1,2),\vec{b}=(t,1)\)のとき、\(\vec{a},\vec{b}\)が垂直となるような定数\(t\)を求めましょう。
[/st-mybox]
[st-slidebox fontawesome=”fa-check” text=”解答をチェックする” bgcolor=”#f1f1f1″ color=”#1a1a1a” margin_bottom=”20″]
\(|\vec{a}|=\sqrt{1^{2}+2^{2}}=\sqrt5\)
\(|\vec{b}|=\sqrt{t^{2}+1^{2}}=\sqrt{t^{2}+1}\)
また、\(\vec{a} \cdot \vec{b}=1 \times t+2 \times 1=t+2\)
\(\vec{a},\vec{b}\)が垂直でならば、\(\cos \theta=0\)となり、
\[\vec{a} \cdot \vec{b}=0\]
よって、
\[t+2=0\]
したがって、\(t=-2\)
[/st-slidebox]
垂直の場合は、\(\cos\theta=0\)になるため、\(|\vec{a}|,|\vec{b}|\)は計算する必要がありませんでしたね。
次の章では、垂直条件を使った問題も紹介します。
 高校生
高校生なす角の求め方がだいぶ分かってきました!
 シータ
シータ素晴らしいね!覚えているうちに、たくさん練習しよう!
ベクトルの内積公式の応用
以前も少し解説しましたが、ここからは、内積の垂直条件と平行条件に付いて解説します。
今回解説した2つのベクトルのなす角とも関連性があるので、復習しておきましょう。
内積の垂直条件
0ではない2つのベクトル\(\vec{a}、\vec{b}\)があります。
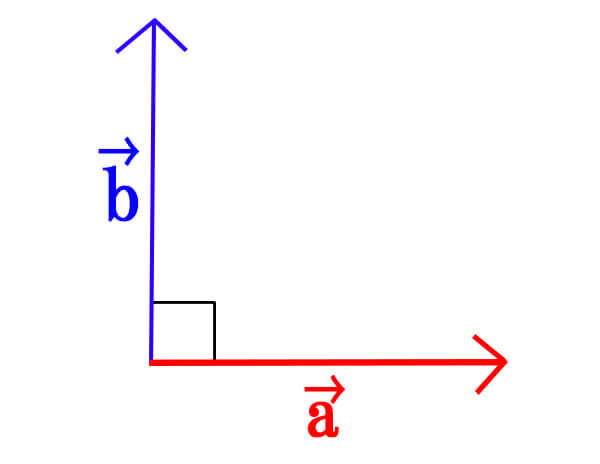
この2ベクトルが垂直に交わるとき、
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#f3f3f3″ borderwidth=”0″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
\[\vec{a}\bot\vec{b} \Leftrightarrow \vec{a} \cdot \vec{b}=0 \Leftrightarrow x_{1}x_{2}+y_{1}y_{2}\]
[/st-mybox]
実際、垂直条件を使った例題を紹介します。
[st-mybox title=”例題” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
0ではない2つのベクトル\(\vec{a},\vec{b}\)があり、\(2|\vec{a}|=|\vec{b}|\)である。
\(3\vec{a}+\vec{b}\)と\(\vec{a}-2\vec{b}\)が垂直となる時、\(\vec{a},\vec{b}\)のなす角\(\theta\)を求めてみましょう。
[/st-mybox]
2つのベクトルが垂直である条件を使うと、
\((3\vec{a}+\vec{b}) \bot (\vec{a}-2\vec{b})\) より、
\[(3\vec{a}+\vec{b}) \cdot (\vec{a}-2\vec{b})=0\]
ゆえに
\begin{eqnarray}
(3\vec{a}+\vec{b}) \cdot (\vec{a}-2\vec{b})&=&3|\vec{a}|^{2}-5\vec{a} \cdots \vec{b}-2|\vec{b}|^{2}\\
&=&0
\end{eqnarray}
\(2|\vec{a}|=|\vec{b}|\)なので
\begin{eqnarray}
3|\vec{a}|^{2}-5\vec{a} \cdot \vec{b}-8|\vec{a}|^{2}&=&0\\
5\vec{a} \cdot \vec{b}&=&-5|\vec{a}|^{2}\\
\vec{a} \cdot \vec{b}&=&-|\vec{a}|^{2}
\end{eqnarray}
\(\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}|\cos{\theta}\)であるから、
\begin{eqnarray}
\displaystyle \cos{\theta}&=&\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}\\
\displaystyle &=&-\frac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot 2|\vec{a}|}\\
\displaystyle &=&-\frac{1}{2}\\
\theta&=&120°
\end{eqnarray}
内積の平行条件
0ではない2つのベクトル\(\vec{a}=(x_{1},y_{1}),\vec{b}=(x_{2},y_{2}\)があるとき
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#f3f3f3″ borderwidth=”0″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
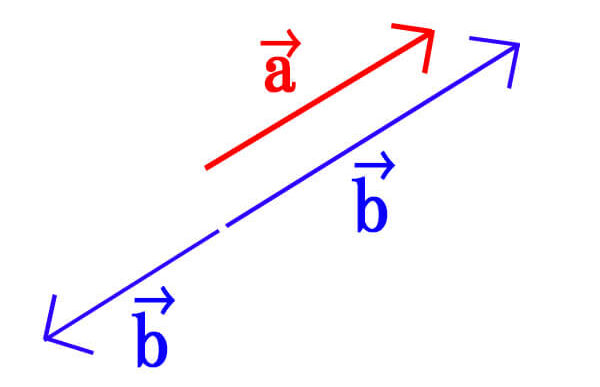
\[\vec{a}//\vec{b} \Leftrightarrow \vec{b}=k\vec{a}\]
\[\vec{a}//\vec{b} \Leftrightarrow x_{1}y_{2}-x_{2}y_{1}=0\]
となる実数kがある。
[/st-mybox]
実際、平行条件を使った例題を紹介します。
[st-mybox title=”例題” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
0ではない2つのベクトル\(\vec{a},\vec{b}\)がある。
\(\vec{a}=(1,2t),\vec{b}=(t,t^{2}+1)\)が平行となる時、\(t\)を求めましょう。
[/st-mybox]
まず、\(\vec{a},\vec{b}\)は平行であるから、
\begin{eqnarray}
1(t^{2}+1)-2t^{2}&=&0\\
t^{2}&=&1\\
t&=&±1
\end{eqnarray}
[1] \(t=1\)のとき
\(\vec{a}=(1,2),\vec{b}=(1,2)\)である。
このとき\(\cos \theta=1\)より、\(\theta=0°\)
[2] \(t=-1\)のとき
\(\vec{a}=(1,-2),\vec{b}=(-1,2)\)である。
このとき\(\cos\theta=-1\)より、\(\theta=180°\)
したがって、いずれにせよ\(\vec{a},\vec{b}\)が平行であることが分かります。
ベクトルのなす角 まとめ
今回はベクトルのなす角について学習しました。
平面ベクトルの・空間ベクトル両方で角度について考えましたが、まず平面ベクトルから理解を進めると分かりやすいです!
[st-minihukidashi fontawesome=”” fontsize=”” fontweight=”” bgcolor=”#FFB74D” color=”#fff” margin=”0 0 20px 0″ radius=”” position=”” myclass=”” add_boxstyle=””]ベクトルのなす角[/st-minihukidashi]
[st-mybox title=”ベクトルのなす角” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#FFFDE7″ borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

ベクトルのなす角とは、2つのベクトルの始点同士を重ねた場合に作られる\(180^\circ\)以下の角度のこと。
下図のように2ベクトルの始点が重なっていない場合は、一方のベクトルを平行移動して始点を重ねる必要がある。

[/st-mybox]
ベクトルのなす角を求めるには、「ベクトルの内積」についてもしっかりと理解しておく必要があります。
ベクトルの内積はこちらの記事で詳しく解説しています。
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]
[/st-mybox]
それでは最後までご覧いただきありがとうございました。
みんなの努力が報われますように!

