ベクトルの平行条件とその証明！平行なベクトルをマスターしよう！

[st-mybox title=”今回解決する悩み” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”4″ borderradius=8″ titleweight=”bold” fontsize=”110″ myclass=”nayami-box” margin=”40px auto 30px”]

「ベクトルの平行ってなに？」
「平行なベクトルをどう表すの？」

[/st-mybox]

今回は数学Bのベクトルから「ベクトルの平行条件」に関するこんな悩みを解決します。

2つのベクトルが平行のとき、以下の式が成り立ちます。

[st-mybox title=”ベクトルの平行条件” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#fafafa” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

0ではない2つのベクトル\(\vec{a}=(x_{1},y_{1}),\vec{b}=(x_{2},y_{2})\)があるとき、実数\(k\)を用いて

\[\vec{a}//\vec{b} \Leftrightarrow \vec{b}=k\vec{a} \cdots①\]

が成り立つ。

また、

\[\vec{a}//\vec{b} \Leftrightarrow x_{1}y_{2}-x_{2}y_{1}=0 \cdots②\]

も成り立つ。

[/st-mybox]

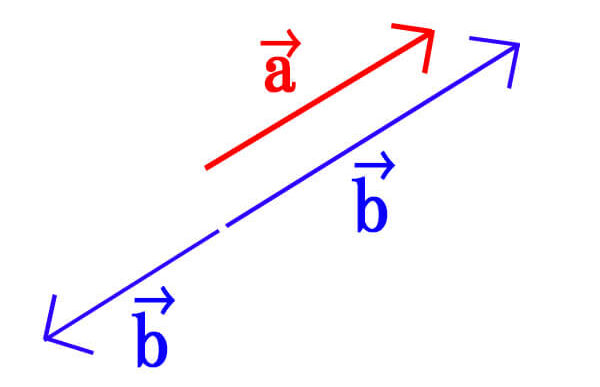
ベクトルが平行ならば、大きさが同じになるように\(k\)倍して調整できるということです。

今回はベクトルの平行条件について詳しく解説していきます。

平行条件の証明や練習問題の紹介など、盛りだくさんながらも分かりやすく説明していきますので、ぜひ最後まで読んで、理解を深めてくださいね！

それではベクトルの平行条件について解説していきましょう。

[st_af id=”13737″]

ベクトルの平行条件

0ではない2つのベクトル\(\vec{a}=(x_{1},y_{1}),\vec{b}=(x_{2},y_{2})\)があるとき、実数\(k\)を用いて

[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#f3f3f3″ borderwidth=”0″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\[\vec{a}//\vec{b} \Leftrightarrow \vec{b}=k\vec{a} \cdots①\]

[/st-mybox]

が成り立つ。

また、

[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#f3f3f3″ borderwidth=”0″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\[\vec{a}//\vec{b} \Leftrightarrow x_{1}y_{2}-x_{2}y_{1}=0 \cdots②\]

[/st-mybox]

も成り立つ。

ここで、\(k\)の値が0より大きいときは、\(\vec{a}\)と\(\vec{b}\)は同じ向きに平行。
\(k\)の値が0より小さいときは、\(\vec{a}\)と\(\vec{b}\)は逆向きに平行です。

平行条件の証明

先ほど紹介した平行条件について、証明していきます。

まずは、ベクトルの平行条件を復習します。

[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

0ではない2つのベクトル\(\vec{a}=(x_{1},y_{1}),\vec{b}=(x_{2},y_{2})\)があるとき、実数\(k\)を用いて

\[\vec{a}//\vec{b} \Leftrightarrow \vec{b}=k\vec{a} \cdots①\]

\[\vec{a}//\vec{b} \Leftrightarrow x_{1}y_{2}-x_{2}y_{1}=0 \cdots②\]

[/st-mybox]

まず、\(\vec{a}//\vec{b} \Leftrightarrow \vec{b}=k\vec{a}…①\)を証明していきます。

[st-slidebox fontawesome=”” text=”+ ①の証明” bgcolor=”#f1f1f1″ color=”#1a1a1a” margin_bottom=”20″]

\(\vec{a} //\vec{b} \rightarrow \vec{b}=k\vec{a}\)から証明します。

２つのベクトルが平行であるということは、ベクトル同士の向きが同じで大きさが異なるか、ベクトル同士の向きが反対で大きさが異なるということ。

よって、実数kを用いて、\(\vec{b}=k\vec{a}\)と表すことができる。

次に\(\vec{b}=k\vec{a} \rightarrow \vec{a} //\vec{b}\)を証明します。

実数\(k\)を用いて、\(\vec{b}=k\vec{a}\)と表せるということは、\(\vec{a}\)と\(\vec{b}\)の向きが同じか反対であるということである。

よってこの場合、\(\vec{a}//\vec{b}\)である。

以上より、\(\vec{a}//\vec{b} \Leftrightarrow \vec{b}=k\vec{a}\)

[/st-slidebox]

次に、\(\vec{b}=k\vec{a} \Leftrightarrow x_{1}y_{2}-x_{2}y_{1}=0…②\)を証明します。

[st-slidebox fontawesome=”” text=”+ ②の証明” bgcolor=”#f1f1f1″ color=”#1a1a1a” margin_bottom=”20″]

\(\vec{b}=k\vec{a} \rightarrow x_{1}y_{2}-x_{2}y_{1}=0\)を証明します。

今、\(\vec{a}=(x_{1},y_{1}),\vec{b}=(x_{2},y_{2})\)であり、\(\vec{b}=k\vec{a}\)となる実数kがあるとき、

\begin{eqnarray}
(x_{2},y_{2})&=&k(x_{1},y_{1})\\
(x_{2},y_{2})&=&(kx_{1},ky_{1})
\end{eqnarray}

ここで、比を考える。

\begin{eqnarray}
x_{2}:y_{2}=kx_{1}:ky_{1} &\Leftrightarrow& x_{2}:y_{2}=x_{1}:y_{1}\\
&\Leftrightarrow& x_{1}y_{2}-x_{2}y_{1}=0
\end{eqnarray}

\(x_{1}y_{2}-x_{2}y_{1}=0 \rightarrow \vec{b}=k\vec{a}\)を証明していきます。

\begin{eqnarray}
x_{1}y_{2}-x_{2}y_{1}=0 &\Leftrightarrow& x_{2}:y_{2}=x_{1}:y_{1}\\
&\Leftrightarrow& x_{2}:y_{2}=kx_{1}:ky_{1}
\end{eqnarray}

これは、\(\vec{b}\)が\(\vec{a}\)のk倍（kは実数）であることを示すので、\(\vec{b}=k\vec{a}\)となる実数kがあるということでもある。

以上より、\(\vec{b}=k\vec{a} \Leftrightarrow x_{1}y_{2}-x_{2}y_{1}=0…②\)

[/st-slidebox]

aベクトルに平行な単位ベクトル

ここからは平行な単位ベクトルについて解説します。

基礎問題としてテストなどで出題されます。よく理解しておきましょう。

まずは、単位ベクトルについて復習しましょう。
単位ベクトルとは、大きさが1のベクトルです。

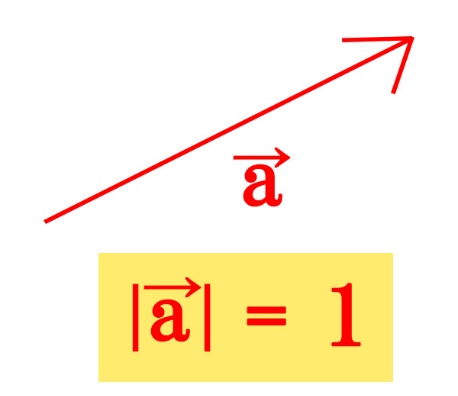
単位ベクトルの定義をおさえながら、例題を見ていきます。

[st-mybox title=”例題” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\(\vec{a}=(2,-1)\)に平行な単位ベクトル\(\vec{t}\)を求めましょう。

[/st-mybox]

求めたい単位ベクトルを\(\vec{t}=(x,y)\)とします。

単位ベクトルですので\(|\vec{t}|=1\)であることから、

\[x^{2}+y^{2}=1\]

また、

\begin{eqnarray}
x_{1}y_{2}-x_{2}y_{1}&=&0\\
2\times y-x\times\left(-1\right)&=&0\\
2y+x&=&0\\
x&=&-2y
\end{eqnarray}

先ほどの、\(x^{2}+y^{2}=1\)を使って、

\begin{eqnarray}
(-2y)^{2}+y^{2}&=&1\\
5y^{2}&=&1\\
y^{2}&=&\frac{1}{5}\\
\displaystyle y&=&\pm \frac{1}{\sqrt5}\\
\displaystyle y&=&\pm \frac{\sqrt5}{5}
\end{eqnarray}

よって、求める単位ベクトルは、

\(\displaystyle \vec{t}=(-\frac{2\sqrt5}{5},\frac{\sqrt5}{5}),(\frac{2\sqrt5}{5},-\frac{\sqrt5}{5})\)

1つのベクトルに対して平行なベクトルは2つありますので、両方とも答えになります。

平行条件を用いた練習問題

ここからは、平行条件を絡めたベクトルの練習問題を紹介していきます。
できるだけ丁寧に解説していきますので、ぜひ一緒に解いてみましょう。

[st-mybox title=”練習問題①” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\(\vec{a}=(2,3),\vec{b}=(6,k)\)とする。

このとき、\(\vec{a},\vec{b}\)が互いに平行となるような\(k\)の値を求めよう。

[/st-mybox]

[st-mybox title=”練習問題②” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\(\vec{a}=(t,-4),\vec{b}=(6,8)\)とする。
このとき、\(\vec{a},\vec{b}\)が互いに平行となるような\(t\)の値を求めよう。

[/st-mybox]

[st-slidebox fontawesome=”fa-check” text=” 解答をチェックする ” bgcolor=”#f1f1f1″ color=”#1a1a1a” margin_bottom=”20″]

\(\vec{a},\vec{b}\)が互いに平行であるとき、\(\vec{b}=k\vec{a}\)となる実数\(k\)がある。

\((6,8)=k(t,-4)\)となる実数\(k\)を考えると、

\begin{equation}
\begin{aligned}
6 & = kt\\
8 & = -4k
\end{aligned}
\end{equation}

したがって、\(k=-2\)であるから\(t=－3\)

[/st-slidebox]

ベクトルの垂直条件

ベクトルの平行条件と合わせて、「ベクトルの垂直条件」についても確認しておきましょう。

0ではない2つのベクトル\(\vec{a}、\vec{b}\)があります。

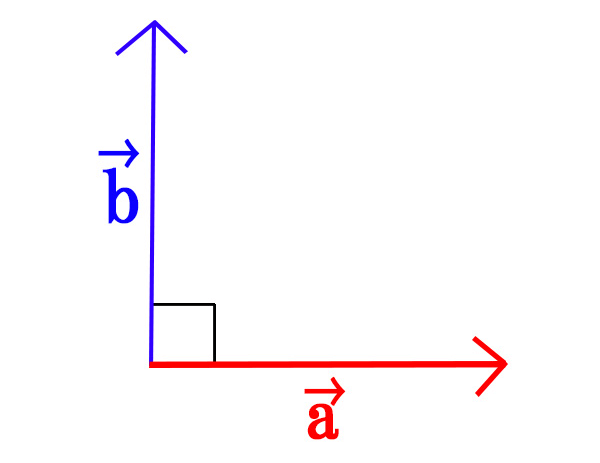
このとき

[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#f3f3f3″ borderwidth=”0″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\[\vec{a} \bot \vec{b} \Leftrightarrow \vec{a} \cdot \vec{b}=0 \Leftrightarrow x_{1}x_{2}+y_{1}y_{2}=0\]

[/st-mybox]

別記事では、この垂直条件について証明・練習問題を紹介していますので、ぜひチェックしてみてください。

[st-card myclass=”” id=”14726″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”on” thumbnail=”on” type=””]

ベクトルの平行条件　まとめ

今回はベクトルの平行条件について学習しました。

[st-minihukidashi fontawesome=”” fontsize=”” fontweight=”” bgcolor=”#FFB74D” color=”#fff” margin=”0 0 20px 0″ radius=”” position=”” myclass=”” add_boxstyle=””]まとめ[/st-minihukidashi]

[st-mybox title=”ベクトルの平行条件” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#FFFDE7″ borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

0ではない2つのベクトル\(\vec{a}=(x_{1},y_{1}),\vec{b}=(x_{2},y_{2})\)があるとき、実数\(k\)を用いて

\[\vec{a}//\vec{b} \Leftrightarrow \vec{b}=k\vec{a} \cdots①\]

が成り立つ。

また、

\[\vec{a}//\vec{b} \Leftrightarrow x_{1}y_{2}-x_{2}y_{1}=0 \cdots②\]

も成り立つ。

ここで、\(k\)の値が0より大きいときは、\(\vec{a}\)と\(\vec{b}\)は同じ向きに平行。
\(k\)の値が0より小さいときは、\(\vec{a}\)と\(\vec{b}\)は逆向きに平行です。

[/st-mybox]

ベクトルの平行条件でも内積は欠かせないので「ベクトルの内積」についてもしっかりと理解しておく必要があります。

ベクトルの内積はこちらの記事で詳しく解説しています。

[st-card myclass=”” id=”14675″ label=”” pc_height=”” name=”” bgcolor=”” color=”” fontawesome=”” readmore=”on” thumbnail=”on” type=””]

[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

>>ベクトルの内積の公式と求め方を解説！

>>ベクトルの成分表示の意味と求め方！

[/st-mybox]

それでは最後までご覧いただきありがとうございました。

みんなの努力が報われますように！