「重心ってなんだけ?」
「重心の性質が知りたい」
今回は重心に関する悩みを解決します。
 高校生
高校生重心ってどんな点だっけ…
三角形には五心という5つの点が存在します。

今回は五心のなかでも“重心”についてまとめました。
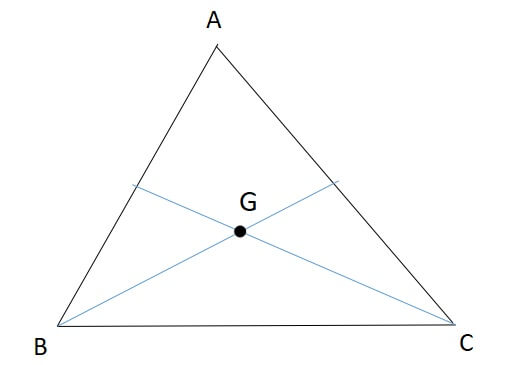
三角形の重心とは、「各頂点から対辺の中点を結んだ線分の交点」を指します。
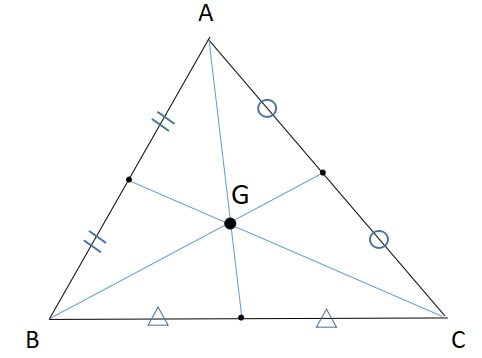
また重心の座標や位置ベクトルは以下の公式で求めることができます。
《重心の座標公式》
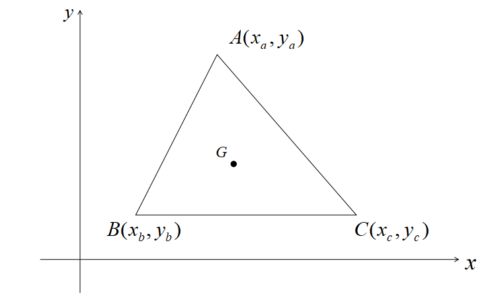
\(\triangle ABC\)において、\(A(x_{a},y_{a}),B(x_{b},y_{b}),C(x_{c},y_{c})\)とすると重心Gの座標は以下のようになります。
\[\displaystyle G(\frac{x_{a}+x_{b}+x_{c}}{3},\frac{y_{a}+y_{b}+y_{c}}{3})\]
《重心の位置ベクトル》
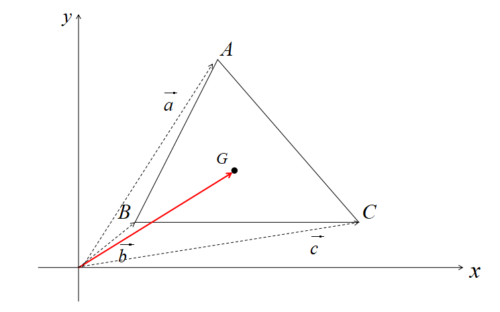
\(\triangle ABC\)において、\(A(\vec{a}),B(\vec{b}),C(\vec{c})\)とすると重心Gの位置ベクトルは以下のようになります。
\[\displaystyle \vec{g}=\frac{\vec{a}+\vec{b}+\vec{c}}{3}\]
本記事では三角形の重心の公式や性質を解説します。
本記事を読めば重心のことがすべて理解できます。重心の疑問がある方はぜひ最後までご覧ください。
それでは三角形の重心について解説していきます。
三角形の重心とは
三角形の重心は、三角形の各頂点から引いた中線の交点です。

三角形における各中線の交点
※辺の中点と向かい合う頂点を結んだ線分を中線といいます。
ここに三角形\(ABC\)があります。
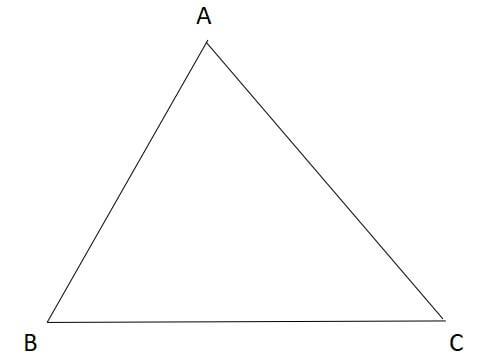
すべての頂点から中線を引きます。

すると、3本の中線が1点で交わります。
この点が三角形の重心です。
 高校生
高校生中線という言葉は初めて聞きました
 シータ
シータこの機会にぜひ覚えておこう!
重心の座標公式
三角形の重心の座標公式について詳しく解説します。
座標公式

\(\triangle ABC\)において、\(A(x_{a},y_{a}),B(x_{b},y_{b}),C(x_{c},y_{c})\)とするとき重心Gの座標は以下の公式で求められます。
\[\displaystyle G(\frac{x_{a}+x_{b}+x_{c}}{3},\frac{y_{a}+y_{b}+y_{c}}{3})\]
重心の座標を求める
\(\triangle ABC\)において、各頂点の座標を\(A(3,5),B(1,1),C(5,2)\)とする。
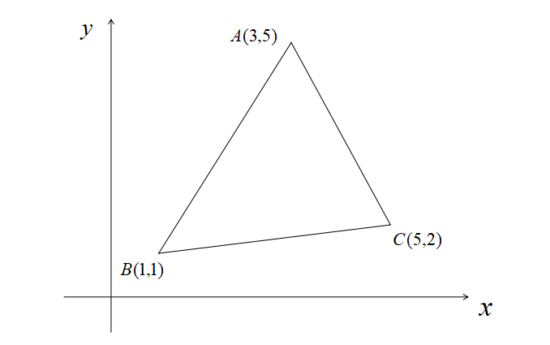
このとき重心Gの座標は、
\[\displaystyle G(\frac{3+1+5}{3},\frac{5+1+2}{3})=(3,\frac{8}{3})\]
三角形の頂点の座標が分かれば、重心の座標は求めることができます。
 シータ
シータ公式を知っていれば簡単だね!
 高校生
高校生なぜ重心の公式は成り立つのですか?
重心の座標公式《証明》
ここで重心の座標公式の証明をしましょう。
\[\displaystyle G(\frac{x_{a}+x_{b}+x_{c}}{3},\frac{y_{a}+y_{b}+y_{c}}{3})\]
\(\triangle ABC\)において、\(A(x_{a},y_{a}),B(x_{b},y_{b}),C(x_{c},y_{c})\)で重心を\(G(x,y)\)とします。

このとき辺BCの中点を点Mとすると、点Mは辺BCを\(1:1\)に内分するので、
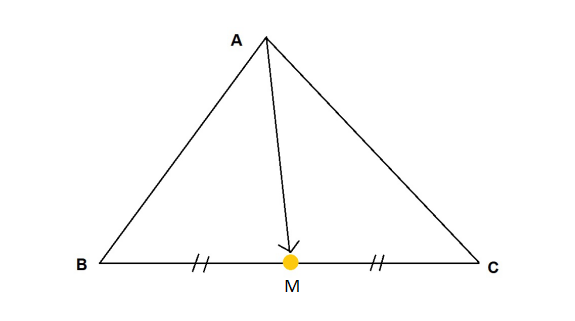
\[\displaystyle M \left(\frac{x_{b}+x_{c}}{2},\frac{y_{b}+y_{c}}{2}\right)\]
重心の性質より、重心Gは線分AMを\(2:1\)に内分するので、
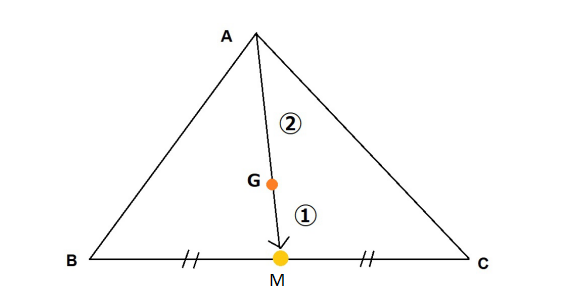
ゆえに、重心Gの座標は
\begin{eqnarray}
\displaystyle G&=&\left(\frac{x_{a}+2 \cdot \frac{x_{b}+x_{c}}{2}}{2+1},\frac{y_{a}+2 \cdot \frac{y_{b}+y_{c}}{2}}{2+1}\right)\\
&=&\left(\frac{x_{a}+x_{b}+x_{c}}{3},\frac{y_{a}+y_{b}+y_{c}}{3}\right)
\end{eqnarray}
したがって、
\[\displaystyle G\left(\frac{x_{a}+x_{b}+x_{c}}{3},\frac{y_{a}+y_{b}+y_{c}}{3}\right)\]
これで重心の座標公式の証明終了です。
重心のベクトル公式
三角形の重心の位置ベクトルについて詳しく解説します。
位置ベクトルの公式

\(\triangle ABC\)において、\(A(\vec{a}),B(\vec{b}),C(\vec{c})\)とすると重心Gの位置ベクトルは以下のようになります。
\[\displaystyle \vec{g}=\frac{\vec{a}+\vec{b}+\vec{c}}{3}\]
位置ベクトルを求める
三角形の各頂点の位置ベクトルを\(A(\vec{a})=(3,6),B(\vec{b})=(1,2),C(\vec{c})=(5,3)\)とします。
このとき、重心Gの位置ベクトル\(G(\vec{g})\)を重心の位置ベクトルの公式に代入して考えましょう。
\[\displaystyle \vec{g}=\frac{\vec{a}+\vec{b}+\vec{c}}{3}\]
\[\displaystyle \vec{g}=(\frac{3+1+5}{3},\frac{6+2+3}{3})\]
したがって、
\[\displaystyle \vec{g}=(3,\frac{11}{3})\]
重心Gの位置ベクトルも求めることができました。
重心の位置ベクトル《証明》
重心の位置ベクトルの公式を求めるにあたって必要な公式があります。
三角形\(\triangle \mathrm{ABC}(\mathrm{A}(\vec{a}), \mathrm{B}(\vec{b}), \mathrm{C}(\vec{c}))\)の内部に点 \(\mathrm{J}(\vec{j})\)をとる。
このとき、\(\triangle \mathrm{JBC},\triangle \mathrm{JCA},\triangle \mathrm{JAB}\)として、それぞれの面積比を
\[\triangle \mathrm{JBC}: \triangle \mathrm{JCA}: \triangle \mathrm{JAB}=p: q: r \quad(p, q, r>0)\]
とする。
このとき
\[\displaystyle \vec{j}=\frac{p \vec{a}+q \vec{b}+r \vec{c}}{p+q+r}\]
が成り立つ。
重心の性質から面積比を考えて、
\(\triangle \mathrm{GBC}: \triangle \mathrm{GCA}: \triangle \mathrm{GAB}=1: 1: 1\)である。
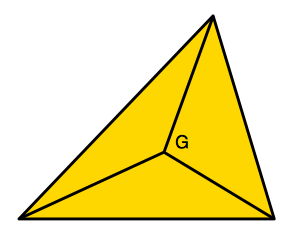
ゆえに,さきほどの公式を活用して、
\(p=q=r=1\)
として考えると
\[\displaystyle \vec{g}=\frac{\vec{a}+\vec{b}+\vec{c}}{3}\]
したがって、重心の位置ベクトルの証明終了。
三角形の重心の性質
三角形の重心には、いくつかの性質があります。
1:頂点と重心を結ぶ線分は対辺を二等分する

2:重心は中線を2:1に内分する
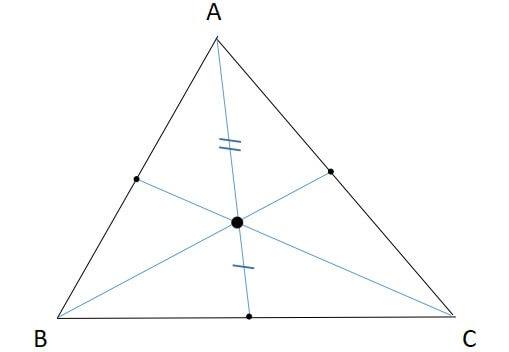
3:内部にできる6つの三角形は面積が等しい

重心の性質《証明》
三角形の重心が持つ性質がなぜそうなるのか証明していきます。
1の「頂点と重心を結ぶと、向かい合う辺を二等分する」は、重心の定義そのままですね。
これはそういうものだと覚えてください。
つぎに2「中線を2:1に内分する」を証明していきます。
これには、中学3年生で習った中点連結定理を使います。
重心と2つの頂点を結ぶと三角形が2つ見えてきます。
このとき、△GBCと△GEDが2:1の相似になります。
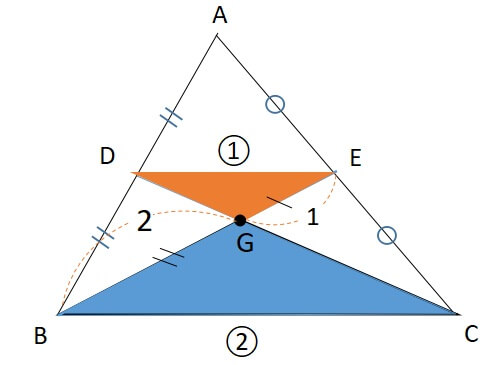
したがって、\(BG:GE=2:1 , CG:GD=2:1\)
角Aでも同様に、\(AG:GF=2:1\)

よって、重心Gは各中線を2:1に内分する。
3:内部にできる6つの三角形は面積が等しいの証明
中線によって,三角形は面積の等しい2つの三角形に分割されます。
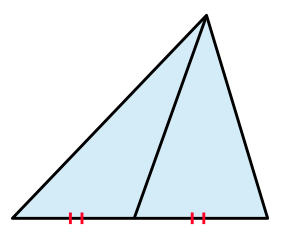
さらに,下の図のように各頂点と重心を結ぶ3直線によって,三角形は面積の等しい3つの三角形に分割されます。

そして,下の図のように3つの中線によって,三角形は面積の等しい6つの三角形に分割される。
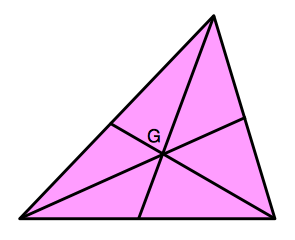
三角形の重心を作図
三角形の重心は、各辺の中線を引くことで作図することができます。
中線を書くには、各辺の中点を見つける必要があります。
必要なのは、三角形、筆記用具、コンパスです。

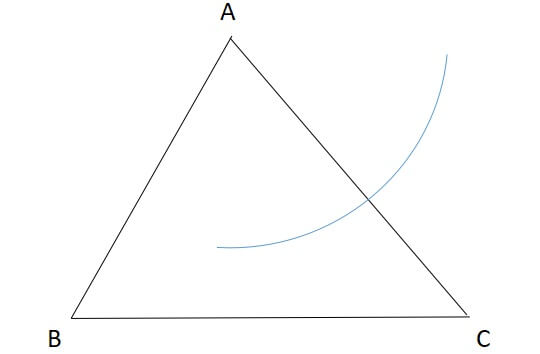
まずどこかの辺を選び、その片方の端点からコンパスで弧を描きます。
このとき、コンパスが描く円の半径は、辺の半分より長くしてください。
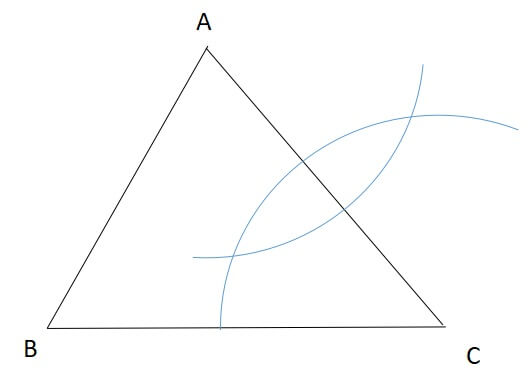
片方で弧が描けたら、コンパスの開きを変えずに、もう片方の端点からも弧を描きます。
すると、2つの弧が交わります。
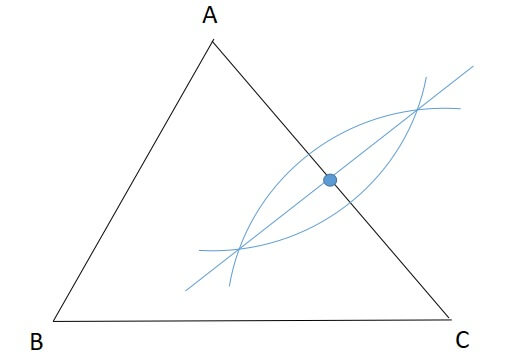
交わった弧の交点を結ぶように直線を引くと、これが垂直二等分線です。
これで中点を見つけることができたので、中点と向かい合う頂点を結んだものが中線です。
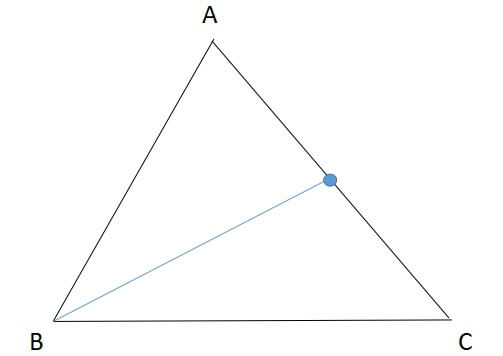
同様に他の辺でも中線を引いて、交わった点が重心です。
3つ目の辺の中線を引いても同じ点で交わるのでタイムロスです。
三角形の重心 まとめ
今回は三角形の重心についてまとめました。

三角形における各中線の交点
- 頂点と重心を結ぶ線分は対辺を二等分する
- 重心は中線を2:1に内分する
- 内部にできる6つの三角形は面積が等しい
重心の定義や性質は知っているものとして問題が出されます。
三角形の重心はベクトルでもよく出てくるので、しっかりと理解しておきましょう。
また、「内心」や「外心」も重要な点なので必ず押さえておきましょう。

