「外心の性質ってなんだっけ?」
「外心の位置ベクトルが分からない」
今回は外心に関する悩みを解決します。
 高校生
高校生三角形の外心ってどんな点だっけ…
三角形には五心と呼ばれる5つの点があります。

今回解説する「外心」は五心の重要な点の1つです。
三角形の外心とは、「三角形の各辺の垂直二等分線の交点」を指します。
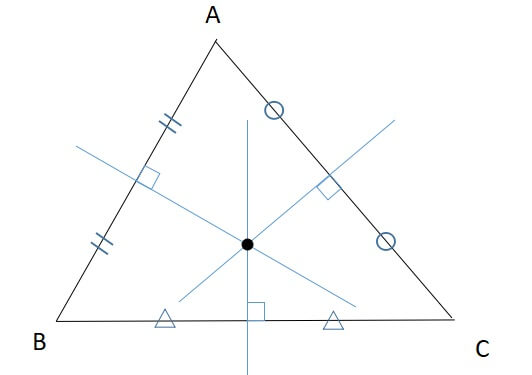
三角形の垂直二等分線を引くと、1点で交わるのです。
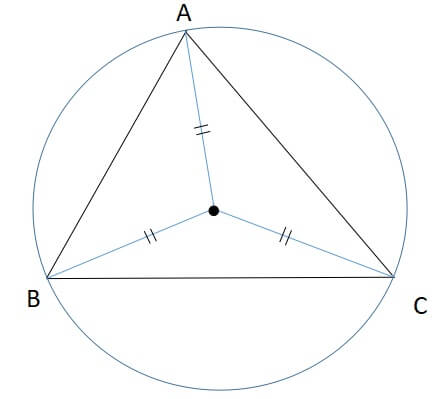
また、外心は三角形の外接円の中心です。
本記事では三角形の外心の定義や性質を解説します。
外心の疑問がある方はぜひ最後までご覧ください。
三角形の外心とは
三角形の外心とは、三角形の各辺の垂直二等分線の交点を指します。

各辺の垂直二等分線の交点
下図のような三角形\(ABC\)があるとしましょう。
この三角形のすべての辺に垂直二等分線を引きます。

すると、3本の垂直二等分線が1点で交わります。
この点を三角形の“外心”と呼びます。
また、三角形の各頂点を通る円を「外接円」といいます。

外心には「外接円の中心」という性質があります。
 シータ
シータ各辺の垂直二等分線で外心を見つけられるよ
外心の位置ベクトル
外心の位置ベクトルは以下のように表されます。
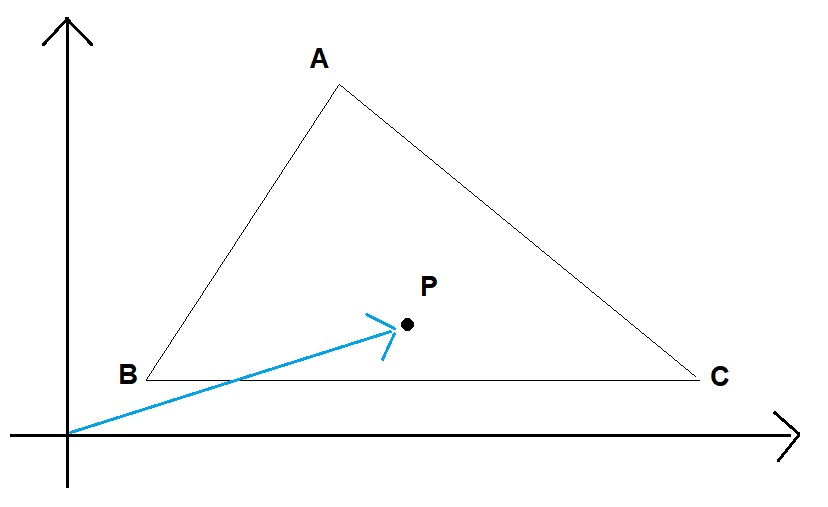
\(\triangle ABC\)の頂点の位置ベクトルを\(\mathrm{A}(\vec{a}), \mathrm{B}(\vec{b}), \mathrm{C}(\vec{c})\)として、心の位置ベクトルを\(P(\vec{p})\)とすると、
\[\displaystyle \vec{p}=\frac{\vec{a} \sin 2 A+\vec{b} \sin 2 B+\vec{c} \sin 2 C}{\sin 2 A+\sin 2 B+\sin 2 C}\]
外心の位置ベクトル《証明》
三角形の外心の位置ベクトルを証明しましょう。

位置ベクトルの公式を証明するにあたって、確認しておきたいことがあります。
三角形\(\triangle \mathrm{ABC}(\mathrm{A}(\vec{a}), \mathrm{B}(\vec{b}), \mathrm{C}(\vec{c}))\)の内部に点 \(\mathrm{J}(\vec{j})\)をとる。
この時\(\triangle \mathrm{JBC},\triangle \mathrm{JCA},\triangle \mathrm{JAB}\)としてそれぞれの面積比を
\(\triangle \mathrm{JBC}: \triangle \mathrm{JCA}: \triangle \mathrm{JAB}=p: q: r \quad(p, q, r>0)\)とする。
このとき
が成り立つ。
これを活用して外心の位置ベクトルの公式を証明します。
\(\triangle ABC\)の外接円の中心を点\(P\)、半径を\(R\)とする。
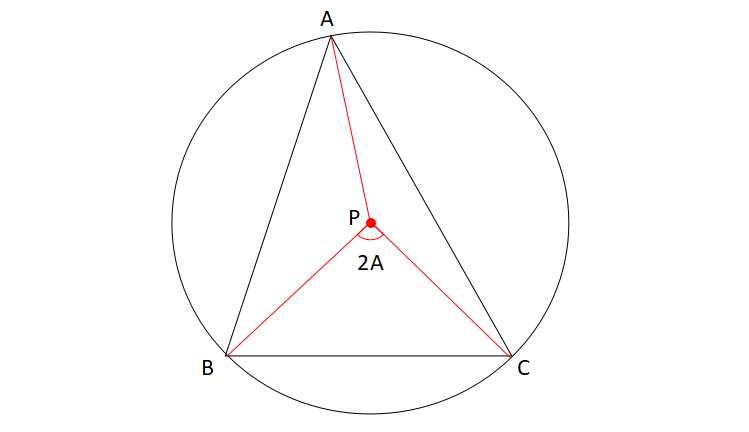
このとき、三角形の面積比は
\begin{eqnarray}
&&\displaystyle \triangle PBC: \triangle PCA: \triangle PAB\\
&=&\frac{1}{2} R^{2} \sin 2 A: \frac{1}{2} R^{2} \sin 2 B: \frac{1}{2} R^{2} \sin 2 C\\
&=&\sin 2 A: \sin 2 B: \sin 2 C
\end{eqnarray}
ここで先ほど確認した三角形の位置ベクトルと面積比の公式より、
\(p=\sin 2 A, q=\sin 2 B,r=\sin 2 C\)とすると、
\[\displaystyle \vec{p}=\frac{\vec{a} \sin 2 A+\vec{b} \sin 2 B+\vec{c} \sin 2 C}{\sin 2 A+\sin 2 B+\sin 2 C}\]
これで、証明終了です。
 高校生
高校生難しくてよく分からなかったです…
 シータ
シータ難しいところなので、ひとまず飛ばしても大丈夫です
三角形の外心《性質》
三角形の外心には、いくつかの性質があります。
- 各辺に垂線を引くと2等分する
- 各頂点からの距離が等しい
- 外接円の中心
1:各辺に垂線を引くと2等分する

2:各頂点からの距離が等しい
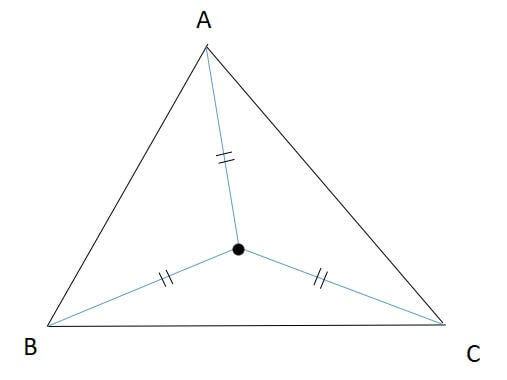
3:外接円の中心

これは2の性質より、各頂点までの距離を半径とすることで円が見えてきます。
したがって、三角形の外心は外接円の中心でもあるのです。
✅ 三角形の五心まとめ記事
三角形の五心(内心、外心、重心、垂心、傍心)性質まとめ
外心の性質《証明》
三角形の外心が持つ性質をなぜそうなるのか証明していきます。
1の「各辺に垂線を引くと2等分する」は、外心の定義「各辺の垂直二等分線の交点」の言い換えですね。
「外心から垂線を引くと2等分する」
「外心と各辺の中点は垂直に交わる」
このどちらともいえます。
つぎに2「各頂点からの距離が等しい」を証明していきます。
外心と2つの頂点を結ぶと三角形が見えてきます。
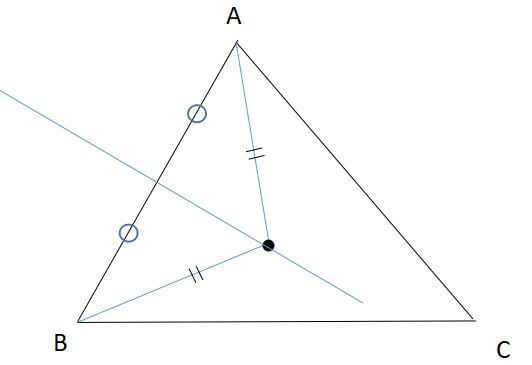
垂直二等分線を引くことで、三角形が2つに分けられます。
この2つの三角形は、2辺とその間の角がそれぞれ等しいので、合同になります。
したがって、\(OA=OB\)

他の頂点でも、同様に二等辺三角形になり、\(OA=OC\)
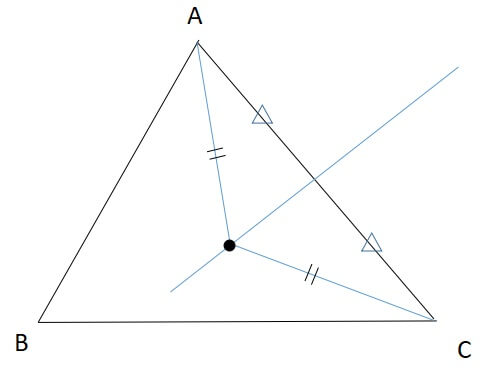
よって、\(OA=OB=OC\)となり、外心は各頂点からの距離が等しいことが証明されました。

3「外接円の中心」は2の性質を応用すると、簡単に証明できます。
2の\(OA=OB=OC\)より3点すべて等距離にあるので、外心を円の中心として、円を描くことができます。

したがって、外心は外接円の中心であることが分かりました。
内心と外心の違い
“内心”と“外心”はよく出てくる点なので、違いを理解しておきましょう。
外心は三角形の外接円の中心ですが、内心は内接円の中心となる点です。
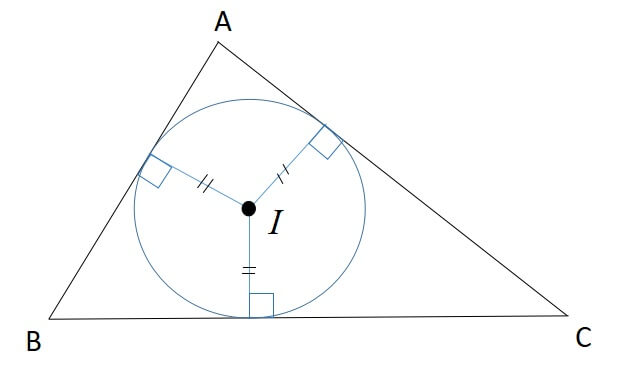
また、内心は角の二等分線の交点です。
三角形の内心の性質は以下のようなものがあります。
- 角を二等分する
- 内心から各辺までの距離が等しい
- 内接円の中心
| 内心 | 外心 |
|---|---|
| 角の二等分線の交点 | 垂直二等分線の交点 |
| 内接円の中心 | 外接円の中心 |
内心については「 三角形の内心の性質と証明」で詳しく解説しています。
 高校生
高校生外心は中線の交点なんですね!
 シータ
シータそうなんだよ!外心も一緒に理解しておこう!
三角形の外心の見つけ方
三角形の外心は、各辺の垂直二等分線を書くことで見つけることができます。
必要なものは三角形、筆記用具、コンパスです。
まずどこかの辺を選び、その片方の端点からコンパスで弧を描きます。
このとき、コンパスが描く円の半径は、辺の半分より長くしてください。
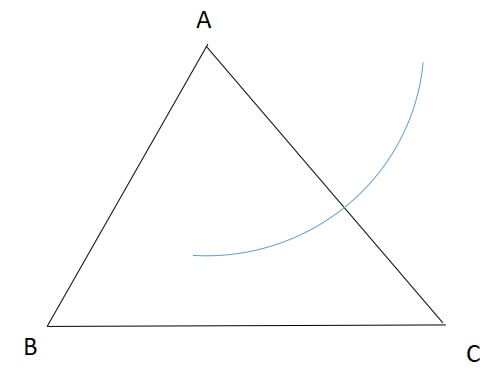
片方で弧が描けたら、コンパスの開きを変えずに、もう片方の端点からも弧を描きます。
すると、2つの弧が交わります。
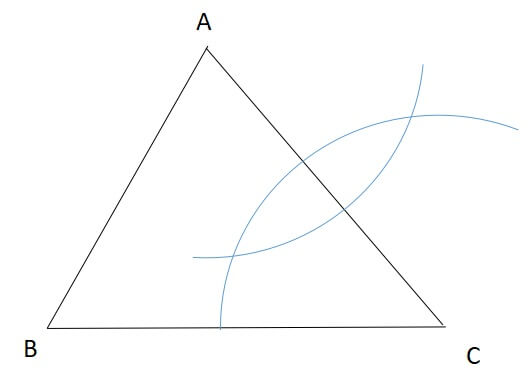
交わった弧の交点を結ぶように直線を引くと、これが垂直二等分線です。
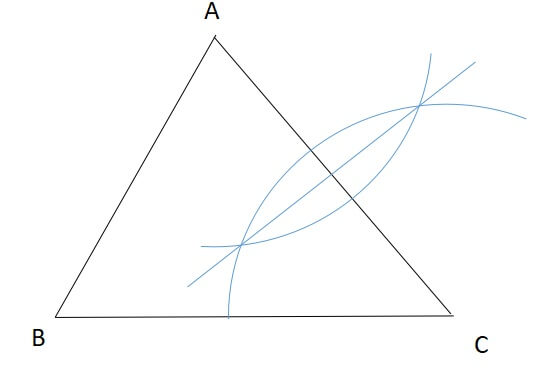
同様に他の辺でも垂直二等分線を引いて、交わった点が外心です。
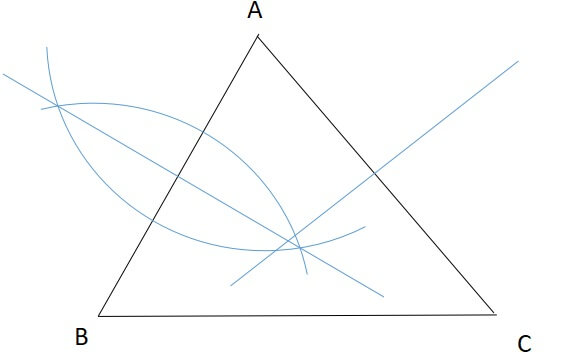
3つ目の辺でも同じことをやっても良いですが、同じところで交わるのでタイムロスです。
三角形の外心 まとめ
今回は五心の中から「外心」をピックアップして解説しました。

定義:三角形の各辺の垂直二等分線の交点
三角形の外心はよく出てくる点なので、性質も覚えておきましょう。
- 各辺に垂線を引くと2等分する
- 各頂点からの距離が等しい
- 外接円の中心
外心の定義や性質は知っているものとして問題が出されます。
今回は五心のなかから”外心”に焦点を当てて解説しました。
「重心」や「垂心」も重要な点なので、必ず理解しておきましょう。

