異なるn個からr個を並べる順列nPrを算出します。
n,rを入力後、算出ボタンクリックしてください。
順列 P = 通りになります。
入力条件を満たしてください。(n≧r>0)
 高校生
高校生計算に困っていたので助かりました!
今回は順列に関するこんな悩みを解決します。
「順列の公式ってなんだっけ?」
「順列の使い方がよく分からない」
 高校生
高校生順列の問題がすごく苦手なんですよ…
数学Aでは順列や組み合わせを用いて事象の場合の数を求めます。
順列Pは以下のような問題で活用します。
4枚のカード「1」「2」「3」「4」があります。
この4枚のカードの中から3枚を使って、3ケタの自然数を作るとき、全部で何通りの数字を作ることができますか?
ここで使いたいのが順列という考え方です。
本記事では、順列の公式とその使い方を5分でサクッと解説します。
順列の公式

まず順列の定義から確認します。
順列
異なる\(n\)個のものから異なる\(r\)個を取り出して並べるときの並べ方
“順”番に”列”にするから順列なのです。
順列の総数とは、並べ方のパターンの総数を指しています。
その順列の総数を\(_{n}P_{r}\)と表します。
\[_{n}P_{r}=n(n-1)(n-2)…..(n-r+1)\]
スタートの\(n\)から1ずつ数字を下げて\(r\)個の項の積を求めます。
例えば\(_{6}P_{3}\)の場合
\[_{6}P_{3}=6\times{5}\times{4}=120\]
このようにPの左下の数から1ずつ数字を下げていき、Pの右側についている個数の項の積を求めます。
 高校生
高校生なんとなくわかった気がするよ!
次に順列の公式の使い方を解説します。
順列の使い方

順列の公式を確認したので、次は順列の使い方を解説します。
冒頭の問題を思い出してください。
ここに4枚のカード「1」「2」「3」「4」があります。

この4枚のカードの中から3枚を使って、3ケタの自然数を作るとき、全部で何通りの数字を作ることができますか?
この問題のポイントは、「3ケタの数字を作る」ではなく「左から3つ数字を並べる」と考えましょう。
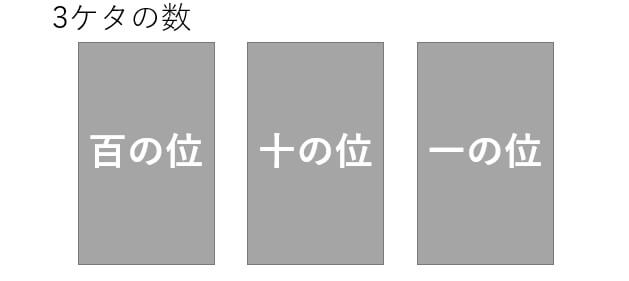
そうすると、4枚のカードの中から3枚を取り出して並べる順列の問題だと分かります。
つまり、\(_{4}P_{3}\)を求めればよいわけです。
\(_{4}P_{3}=4\times{3}\times{2}=24\)
したがって、3ケタの数字の作り方は24通りだと分かりました。
このように、いくつかのものを並べるときの並べ方を求めるときに順列は使われます。
順列の公式<練習問題>

これで終わってしまうとまだ不安な方もいるでしょう。
もう少し順列の考えを使って練習しましょう。
- 7人から3人選んで1列に並べるとき、並べ方の総数を求めよ。
- 10人の生徒から委員長、副委員長、書記を選ぶとき、選び方は何通りありますか。
1.先頭、真ん中、最後尾の3か所に3人を並べればよいので
\[_{7}P_{3}=7\times{6}\times{5}=210\]
A.210通り
2.10人の中から、委員長、副委員長、書記の3か所に3人を並べるので
\[_{10}P_{3}=10\times{9}\times{8}=720\]
A.720通り
順列の公式と使い方 まとめ
今回は数学Aの順列Pの公式と使い方についてまとめました。
異なる(n)個のものから異なる(r)個を取り出して並べるときの並べ方
順列は難しいものではありません。
カードや数字を並べて、その順番によって異なるパターンになるなら順列の問題です。
順列と組み合わせの違いがよく分からない方は「順列と組み合わせの違いと”簡単”な見分け方」にて詳しく解説しています。
場合の数をマスターするには、それぞれの公式や意味を理解する必要があります。
場合の数と確率についてまとめているのでぜひご覧ください。

