「内心ってどんな点だっけ」
「内心の性質が知りたい」
今回は内心に関するこんな悩みを解決します。
 高校生
高校生内心の定義や性質が知りたくて…
三角形には五心という5つの点が存在します。

五心の中でも「内心」や「重心」はよく出題される重要な点ですね。
三角形の内心とは、「三角形の3つの内角の二等分線の交点」を指します。
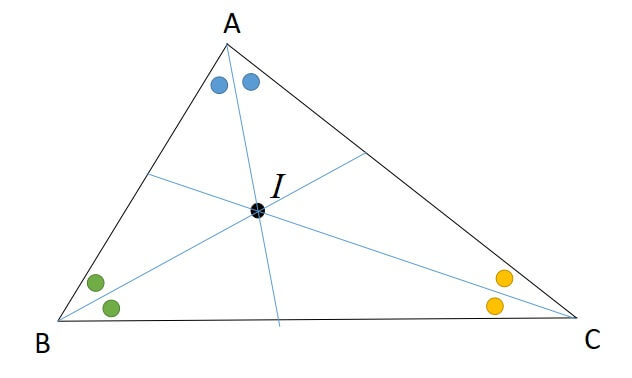
また内心の座標や位置ベクトルは以下の公式で求めることができます。
ただし、公式に代入しただけでは減点対象なので記述問題の検算に活用してください。
《内心の座標公式》
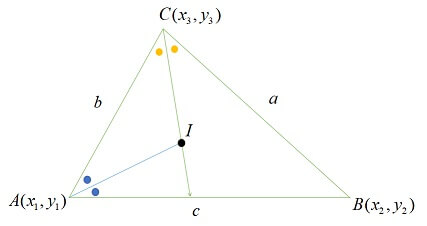
\(\triangle ABC\)において、\(A(x_{a},y_{a}),B(x_{b},y_{b}),C(x_{c},y_{c})\)とすると内心\(I\)の座標は以下のようになる。
\[\displaystyle I \left(\frac{ax_{a}+bx_{b}+cx_{c}}{a+b+c},\frac{ay_{a}+by_{b}+cy_{c}}{a+b+c}\right)\]
《内心の位置ベクトル》
\(\triangle ABC\)において、\(A(\vec{a}),B(\vec{b}),C(\vec{c})\)とすると内心\(I\)の位置ベクトル\(\vec{i}\)は以下のようになる。
[\displaystyle \vec{i}=\frac{a \vec{a}+b \vec{b}+c \vec{c}}{a+b+c}]
本記事では、三角形の内心の定義や性質などを解説しています。
内心に関する疑問がある方はぜひ最後までご覧ください。
三角形の内心とは
三角形の内心とは、三角形の3つの内角の二等分線の交点を指します。
例えばこの点です。
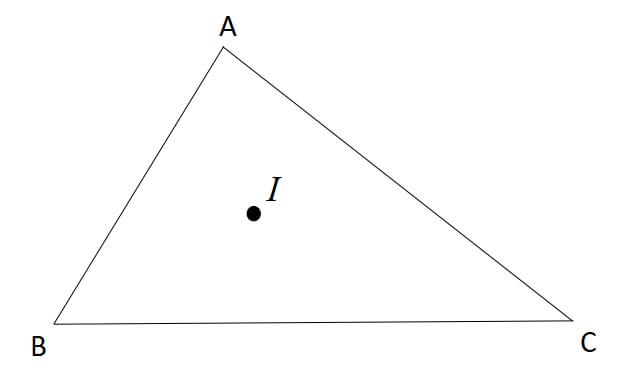
この点、適当に描いた点ではありません。

各角の2等分線を引いた結果、交わった交点なのです。
これが、三角形の内心です。
三角形の内側に接する円のことを「内接円」と呼びます。
内心には「内接円の中心である」という性質があります。
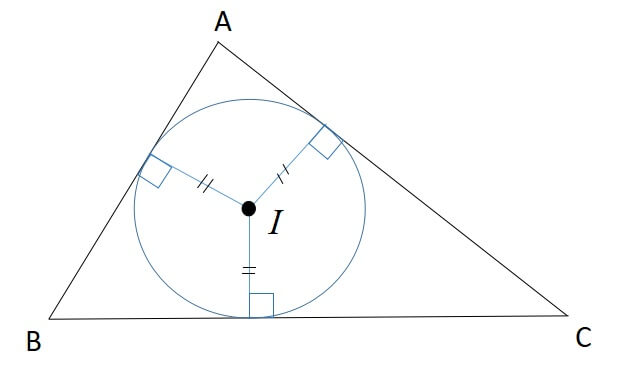
このあと内心の性質について詳しく解説します。
内心と外心の違い
“内心”と”外心”はよく出てくる点なので、違いを理解しておきましょう。
内心は三角形の内接円の中心ですが、外心は外接円の中心となる点です。
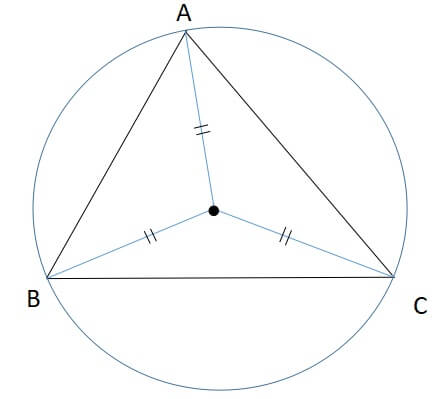
また、外心は各辺の垂直二等分線の交点です。
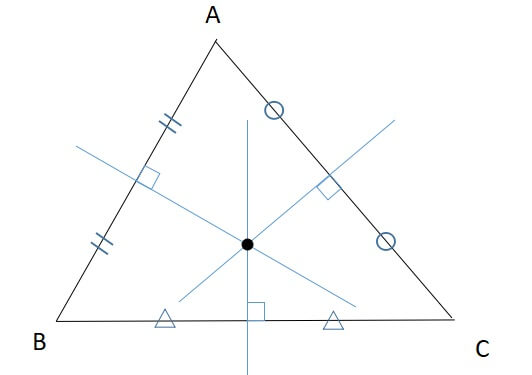
内心と外心の性質を簡単にまとめました。
| 内心 | 外心 |
|---|---|
| 角の二等分線の交点 | 垂直二等分線の交点 |
| 内接円の中心 | 外接円の中心 |
外心については「外心の性質と証明」で詳しく解説しています。
 高校生
高校生外心は中線の交点なんですね!
 シータ
シータそうなんだよ!外心も一緒に理解しておこう!
内心の座標公式
それでは内心の公式について解説していきます。
まずは内心の座標公式を確認しましょう。
座標公式

\(\triangle ABC\)において、\(BC=a,AC=b,AB=c,A(x_{a},y_{a}),B(x_{b},y_{b}),C(x_{c},y_{c})\)とすると内心\(I\)の座標は以下の公式で求められます。
[\displaystyle I \left(\frac{ax_{a}+bx_{b}+cx_{c}}{a+b+c},\frac{ay_{a}+by_{b}+cy_{c}}{a+b+c}\right)]い
ただし、公式に数字を代入しただけでは減点対象なので注意してください。
 シータ
シータ記述問題のときは、途中式もしっかり書こう!
内心の座標を求める
\(\triangle ABC\)において、各頂点の座標を\(A(3,4),B(0,0),C(7,0)\)とする。
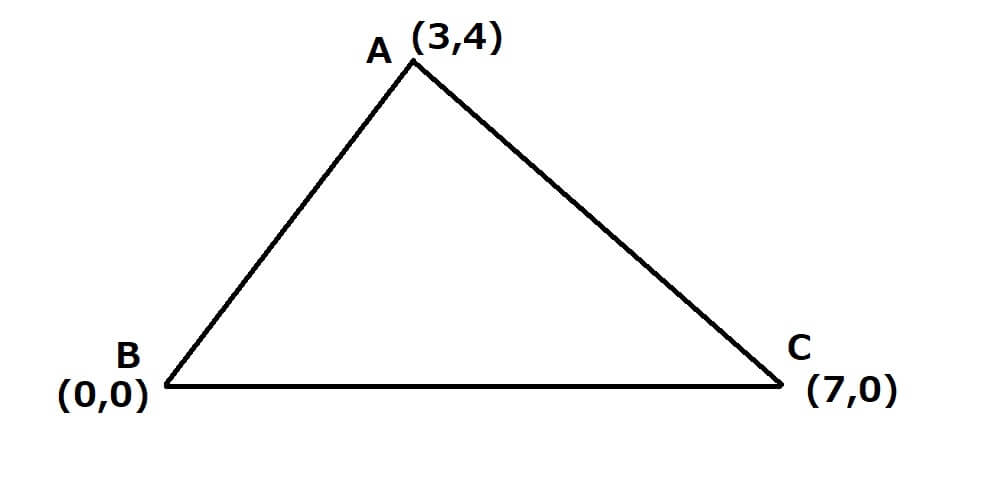
このとき三角形の各辺の長さは
\(BC=7\)
\(AC=\sqrt{(7-3)^{2}+4^{2}}=4\sqrt{2}\)
\(AB=\sqrt{3^{2}+4^{2}=5}\)

したがって、内心の公式に代入すると
\[\displaystyle I \left(\frac{7 \cdot 3+4\sqrt{2} \cdot 0+5 \cdot7}{7+ 4\sqrt{2} +5},\frac{7 \cdot 4+4\sqrt{2} \cdot 0+5 \cdot0}{7+ 4\sqrt{2} +5}\right)\]
したがって、
\[\displaystyle I \left(\frac{14}{3+\sqrt{2}},\frac{7}{3+\sqrt{2}}\right)\]
これで内心の座標を求めることができました。
座標公式の証明
内心\(I\)の座標公式の証明をします。
内心の証明には、内分点の公式を活用します。
\(\triangle ABC\)において、\(BC=a,AC=b,AB=c,A(x_{a},y_{a}),B(x_{b},y_{b}),C(x_{c},y_{c})\)としましょう。
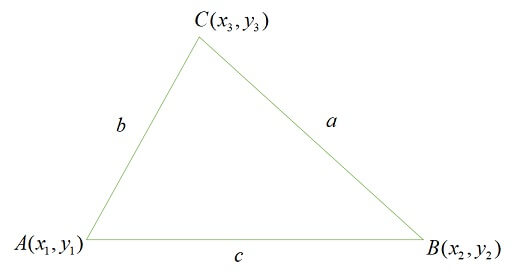
角Cの二等分線と辺ABとの交点を点Dとすると、
\[AD:DB=CA:CB=b:a\]
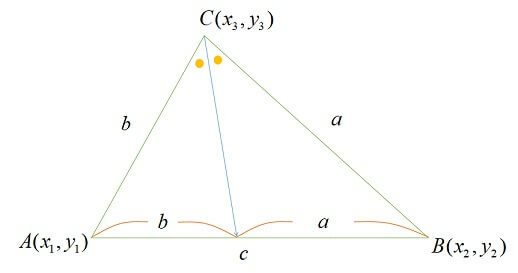
したがって、
\[\displaystyle D \left(\frac{ax_{a}+bx_{b}}{b+a},\frac{ay_{a}+by_{b}}{b+a}\right)\]
また、\(AD:DB=b:a\)より
\[\displaystyle AD=\frac{b}{a+b} AB=\frac{b}{a+b} c\]

つぎに
\[\displaystyle CI:ID=AC:AD=b:\frac{b}{a+b}c=(a+b):c\]
したがって、
\[\displaystyle I\left(\frac{(a+b) \cdot \frac{ax_{a}+bx_{b}}{b+a}+cx_{c}}{(a+b)+c},\frac{(a+b) \cdot \frac{ay_{a}+by_{b}}{b+a}+cy_{c}}{(a+b)+c}\right)\]
となり、内心の座標公式は
[\displaystyle I(\frac{ax_{a}+bx_{b}+cx_{c}}{a+b+c},\frac{ay_{a}+by_{b}+cy_{c}}{a+b+c})]
内心の位置ベクトル
三角形の内心の位置ベクトルについて解説します。
位置ベクトル

\(\triangle ABC\)において、\(A(\vec{a}),B(\vec{b}),C(\vec{c})\)とすると内心Iの位置ベクトルは以下のようになります。
\[\displaystyle \vec{i}=\frac{a \vec{a}+b \vec{b}+c \vec{c}}{a+b+c}\]
内心の位置ベクトルを求める
\(\triangle ABC\)において、\(A(\vec{a})=(3,4),B(\vec{b})=(0,0),C(\vec{c})=(7,0)\)とする。
このとき三角形の各辺の長さは
\(BC=7\)
\(AC=\sqrt{(7-3)^{2}+4^{2}}=4\sqrt{2}\)
\(AB=\sqrt{3^{2}+4^{2}=5}\)
ゆえに内心\(I(\vec{i})\)の位置ベクトルは
\[\displaystyle \vec{i}=\frac{7 \vec{a}+4\sqrt{2} \vec{b}+5 \vec{c}}{7+ 4\sqrt{2} +5}\]
したがって、
\begin{eqnarray}
\displaystyle \vec{i}&=&\frac{7(3,4)+4(0,0)+5(7,0)}{12+ 4\sqrt{2}}\\
\displaystyle &=&\frac{(56,28)}{12+ 4\sqrt{2}}\\
\displaystyle &=&\frac{(14,7)}{3+ \sqrt{2}}
\end{eqnarray}
位置ベクトルの証明
内心の位置ベクトルの公式を求めるにあたって必要な公式があります。
内心の性質から面積比を考えます。
\(\triangle \mathrm{ABC}\)の内接円の半径をrとすると、

面積比 \(\displaystyle \triangle \mathrm{IBC}: \triangle \mathrm{ICA}: \triangle \mathrm{IAB}=\frac{1}{2} a r: \frac{1}{2} b r: \frac{1}{2} \mathrm{cr}=a: b: c\)
ここで先ほど確認した面積比の公式を活用します。
\[\displaystyle \triangle \mathrm{IBC}: \triangle \mathrm{ICA}: \triangle \mathrm{IAB}=a: b: c\]
なので、
\[\displaystyle \vec{i}=\frac{a \vec{a}+b \vec{b}+c \vec{c}}{a+b+c}\]
よって、証明完了です。
 高校生
高校生難しくてよく分からなかったです…
 シータ
シータ分からなかったら飛ばして大丈夫だよ!
三角形の内心《性質》

三角形の内心にはいくつかの性質があります。
- 角を二等分する
- 内心から各辺までの距離が等しい
- 内接円の中心
1:角を二等分する
内心の定義が「内角の二等分の交点」なのですぐに理解できると思います。

2:内心から各辺までの距離が等しい
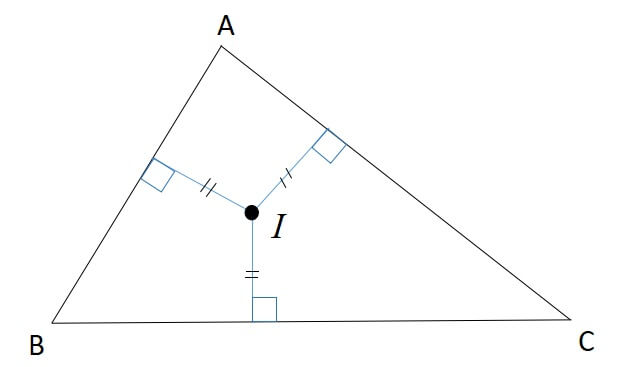
3:内接円の中心

2の応用になりますが、各辺までの距離が等しいということは、そこに円が書けるということです。
したがって、三角形の内心は内接円の中心でもあるのです。
三角形の内心《証明》

では、三角形の内心が持つ性質の証明をします。
1の「角を二等分する」は定義なので、そういうものだと思ってください。
2の「内心から各辺までの距離が等しい」が証明できれば、3の「内接円の中心」であることは円を書けば見えてきますね。
それでは、内心から各辺までの距離が等しくなることを証明していきます。
角の二等分線上に点をとります。
点と辺の距離は垂直に交わる最短の線分なので、角を分けられた二辺に垂線を引くことで、2つの直角三角形ができます。
2つの直角三角形は、斜辺を共有しているため、斜辺と1つの鋭角がそれぞれ等しいので、合同な直角三角形といえます。
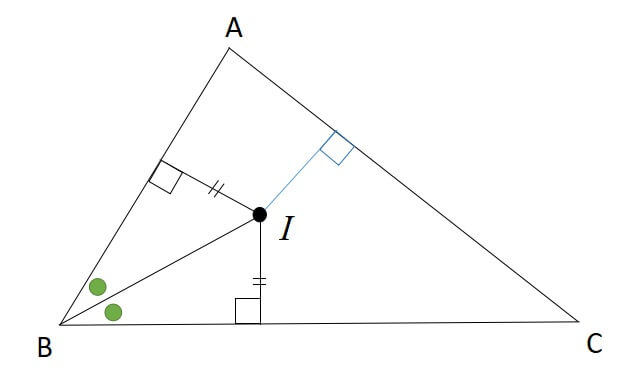
また、同じことを別の三角形でも行うことで、こちらでも点から辺までの距離が等しくなることが確認できました。
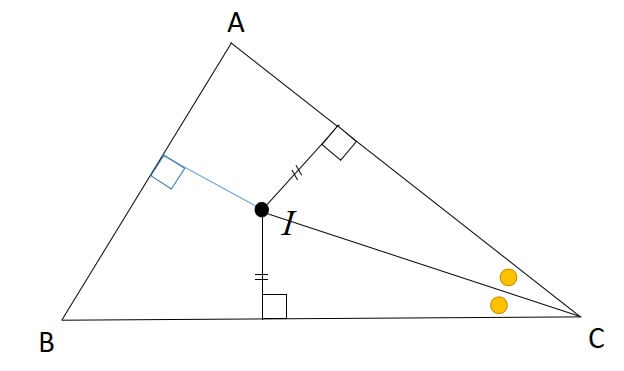
したがって、各角の二等分線の交点である内心は、各辺までの距離が等しいことが証明されました。
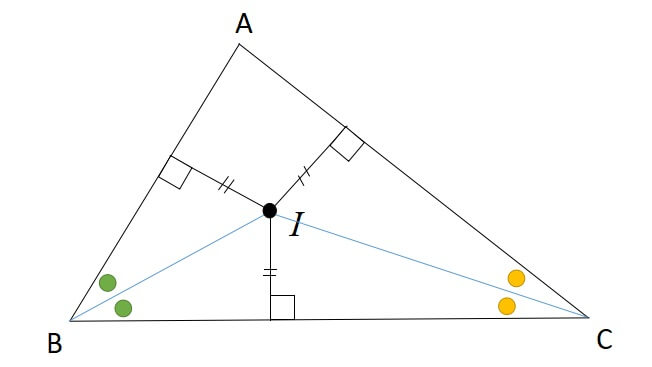
したがって、各辺までの垂線を半径と見たとき、内接円を描くことができ、内心は内接円の中心である。

三角形の内心の見つけ方
三角形の内心は、実際に角の二等分線を引くことで見つけることができます。
角の二等分線の引き方は中学校でも習いましたね。

まず好きな頂点から、弧を描きます。
すると、2つの辺の交わると思います。
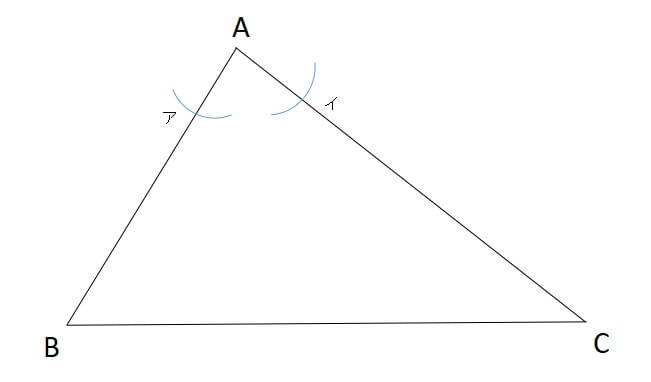
その交点を交点ア、イとでもしましょう。
つぎは交点アに針を置きなおし、再度三角形の内側に弧を描きます。
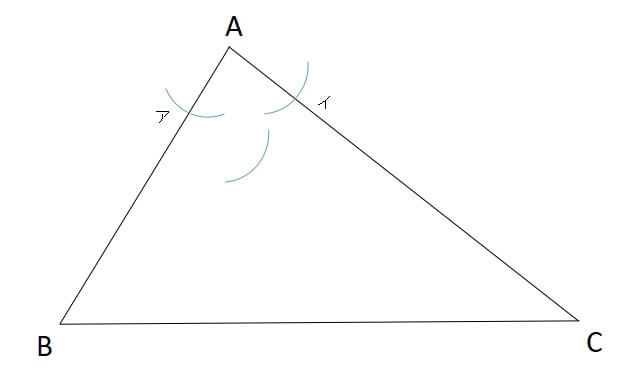
これを交点イでも行います。
すると、お互いの弧が交わるので、初めに選んだ頂点から線を引くと、それが角の二等分線です。
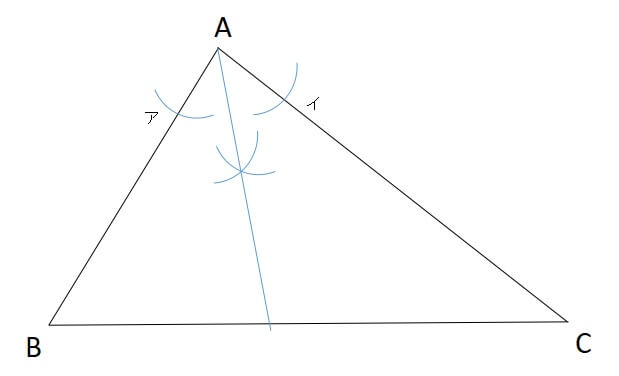
同じことを別の頂点でも行いましょう。
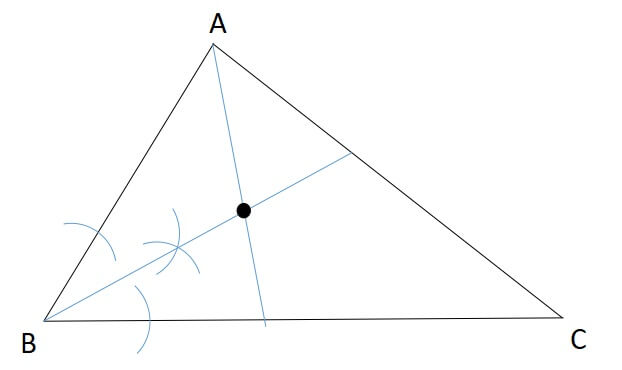
すると、一か所で交わります。
これが、三角形の内心です。
三角形の内心 まとめ
今回は三角形の内心についてまとめました。

三角形の内心はよく出てくる点なので、性質も覚えておきましょう。
内心の定義や性質は知っているものとして問題が出されます。
今回は五心のなかから”内心”に焦点を当てて解説しました。
「重心」や「垂心」も重要な点なので、必ず理解しておきましょう。
その他の五心については別の記事で解説しています。

