数学Ⅰの二次関数ではグラフが必要な問題がたくさんあります。
「2次関数のグラフってどんな形」
「グラフの書き方が分からない」
今回は2次関数のグラフに関するこんな悩みを解決します。
 高校生
高校生2次関数のグラフを書きたいんだけど、書き方が分からなくて…
2次関数のグラフは以下の3ステップで書くと上手に描くことができます。
- 頂点を求める
- y軸との交点を求める
- 頂点とy軸との交点をなめらかに結ぶ
本記事では2次関数のグラフの書き方を解説していきます。
具体例を用意したのでじっくりと読んでもらえば、2次関数のグラフが書けるようになります。
 シータ
シータ気になる見出しをクリックして、
ぜひ最後までご覧ください。
2次関数の基礎
2次関数\(y=ax^{2}+bx+c\)のグラフはこんな形をしています。
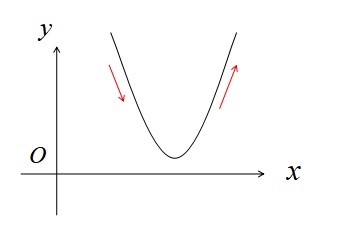
関数\(y=ax^{2}+bx+c\)の中で最も次数が高い項は\(ax^{2}\)ですね。最高次数が2なので2次関数といいます。
\(y=ax+b\)の場合、最も次数が高い項が\(ax\)で次数1なので一次関数といいます。
\(y=ax^{3}+bx^{2}+cx+d\)は三次関数
\(y=ax^{4}+bx^{3}+cx^{2}+dx+e\)は四次関数
2次関数のグラフの形
2次関数のグラフは左右対称な放物線を描きます。

\(y=ax^{2}+bx+c\)のグラフは\(a\)の符号によって形が変わります。
\(a>0\)のとき、下向きに凸な放物線
\(a<0\)のとき、上向きに凸な放物線
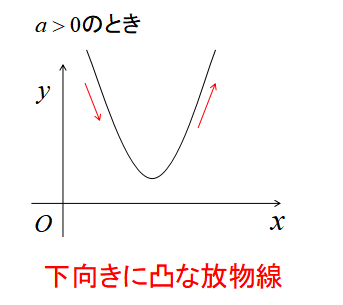
\(a>0\)のとき、下向きに凸な放物線
2次関数\(y=ax^{2}+bx+c\)において\(a\)が正の数ならば、グラフは下向きに凸な放物線になります。
\[y=x^{2}-3x+5\]
\[y=3x^{2}-4x+4\]
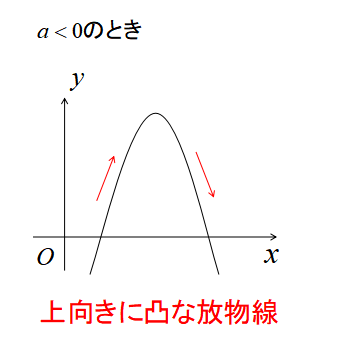
\(a<0\)のとき、上向きに凸な放物線
2次関数\(y=ax^{2}+bx+c\)において\(a\)が負の数ならば、グラフは上向きに凸な放物線になります。
\[y=-x^{2}+3x-5\]
\[y=-3x^{2}+4x-4\]
 高校生
高校生グラフの形は理解できました!
2次関数のグラフの書き方

2次関数のグラフは以下の3ステップで書くことができます。
- 頂点を求める
- y軸との交点を求める
- 頂点とy軸との交点を結ぶ
\(y=x^{2}+6x+5\)を例にして各ステップを詳しく解説します。
STEP1グラフの頂点を求める
まずは頂点の座標を求めます。
2次関数の頂点は関数を平方完成することで求めることができます。
\(y=a(x+p)^{2}+q\)のとき、
軸:\(x=-p\) 、頂点\((-p,q)\)
例として\(y=x^{2}+6x+5\)を平方完成すると
\begin{eqnarray*}
y&=&x^{2}+6x+5\\
&=&(x+3)^{2}-4
\end{eqnarray*}
となります。
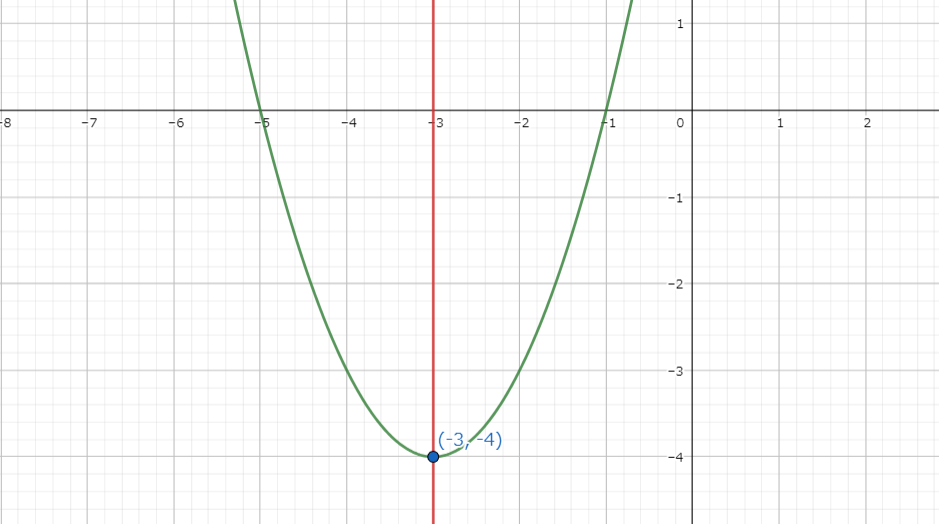
したがって、\(y=x^{2}+6x+5\)の頂点は\((-3,-4)\)となります。

STEP2y軸との交点を求める
頂点の座標が分かっただけでは2次関数のグラフを書くことはできません。
次はグラフとy軸との交点を求めます。
y軸との交点を求める ⇒ 関数に\(x=0\)を代入
y軸上の点ということは、点のx座標が0であることを指します。
\(y=x^{2}+6x+5\)に\(x=0\)を代入すると
\begin{eqnarray*}
y&=&0^{2}+6 \cdot 0+5\\
&=&5
\end{eqnarray*}
したがって、
\(y=x^{2}+6x+5\)のグラフは\((0,5)\)でy軸と交わることが分かりました。
STEP3頂点とy軸の交点を滑らかにつなぐ
最後にSTEP1,2で求めた頂点とy軸との交点を滑らかにつなぎます。
\(y=x^{2}+6x+5\)の頂点は\((-3,-4)\)、y軸との交点は\((0,5)\)でした。
この2点を滑らかにつなぎ、左右対称に描くと2次関数のグラフが完成します。
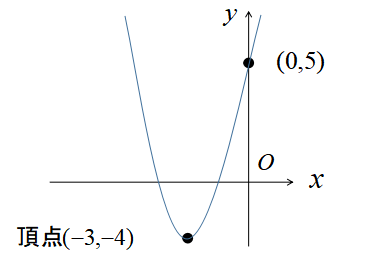
2次関数の式をグラフにできるようになれば、分かっている点から元々の式を求めることもできます。
2次関数のグラフ《練習問題》
2次関数の書き方3ステップを活かして、以下のグラフを書いてみましょう。
- \(y=x^{2}-4x+5\)
- \(y=-x^{2}+6x-4\)
- \(y=2x^{2}+8x+5\)
\(y=x^{2}-4x+5\)のグラフ
まず平方完成して放物線の軸と頂点を求めます。
\begin{eqnarray*}
y&=&x^{2}-4x+5\\
&=&(x-2)^{2}+1
\end{eqnarray*}
したかって、頂点の座標は\((2,1)\)と分かりました。
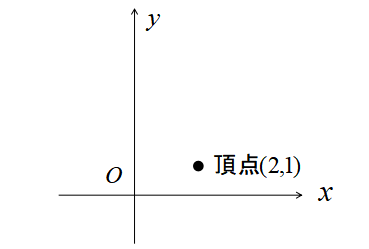
つぎに\(y\)軸との交点を求めます。
\(x=0\)を代入して、
\(y=x^{2}-4x+5=0^{2}-4 \cdot 0 +5=5\)
よって、\(y\)軸との交点は\((0,5)\)だと分かります。

放物線の頂点\((2,1)\)とy軸との交点\((0,5)\)を滑らかにつなぐと完成です。
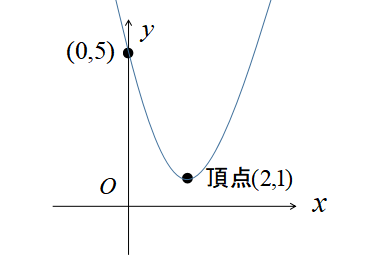
\(y=-x^{2}+6x-4\)のグラフ
まずは平方完成して軸と頂点を求めます。
\begin{eqnarray}
y&=&-x^{2}+6x-4\\
&=&-(x^{2}-6x)-4\\
&=&-\{(x-3)^{2}-9\}-4\\
&=&-(x-3)^{2}+5
\end{eqnarray}
したがって、頂点の座標は\((3,5)\)だと分かりました。
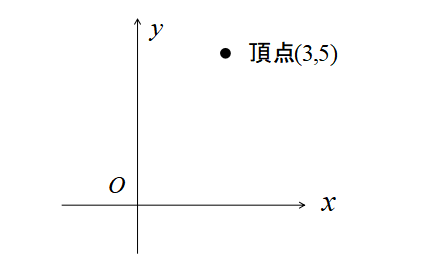
次に\(y\)軸との交点を求めます。
\(x=0\)を代入して、
\(y=-x^{2}+6x-4=0^{2}+6 \cdot 0 -4=-4\)
よって、\(y\)軸との交点は\((0,-4)\)だと分かります。
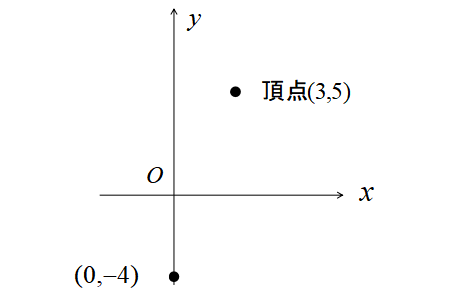
放物線の頂点\((3,5)\)とy軸との交点\((0,-4)\)を滑らかにつなぐと完成です。
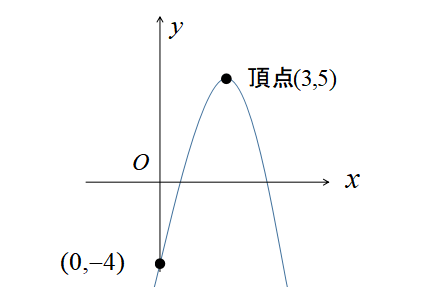
\(y=2x^{2}+8x+5\)のグラフ
まずは平方完成して軸と頂点を求めます。
\begin{eqnarray}
y&=&2x^{2}+8x+5\\
&=&2(x^{2}+4x)+5\\
&=&2\{(x+2)^{2}-4\}+5\\
&=&2(x+2)^{2}-3\\
\end{eqnarray}
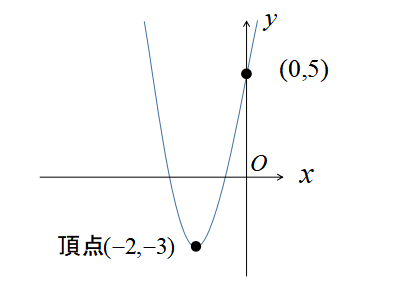
したがって、頂点の座標は\((-2,-3)\)だと分かりました。
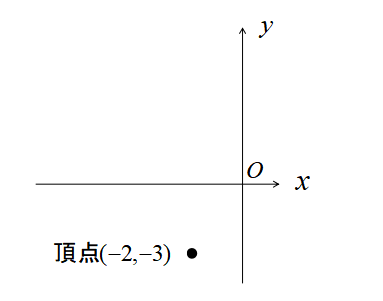
次に\(y\)軸との交点を求めます。
\(x=0\)を代入して、
\(y=2x^{2}+8x+5=2 \cdot 0^{2}+8 \cdot 0 +5=5\)
よって、\(y\)軸との交点は\((0,5)\)だと分かります。
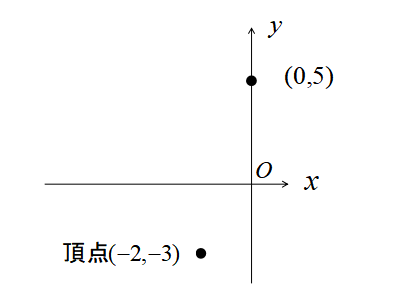
放物線の頂点\((-2,-3)\)とy軸との交点\((0,5)\)を滑らかにつなぐと完成です。
2次関数のグラフ まとめ
今回は2次関数のグラフの書き方についてまとめました。
2次関数のグラフの形
\(a>0\)のとき、下向きに凸な放物線
\(a<0\)のとき、上向きに凸な放物線
2次関数のグラフの形
\(a>0\)のとき、下向きに凸な放物線
\(a<0\)のとき、上向きに凸な放物線
グラフを書く手順
1.軸と頂点を求める
2.y軸との交点を求める
3.頂点とy軸との交点を滑らかにつなぐ
2次関数のグラフが書けないと、最大値・最小値を求める問題でかなり苦戦します。
決して難しい手順ではないので、必ずグラフを書けるようにしましょう。
それでは最後までご覧いただきありがとうございました。
みんなの努力が報われますように!

