対数不等式の解き方と注意点！《5つのパターンを徹底解説》

[st-mybox title=”” fontawesome=”fa-question-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

「対数不等式の解き方が分からない」

「底に文字があるときはどうするの？」

[/st-mybox]

対数の不等式が解けない方は必見です！

今回は対数不等式に関するこんな悩みを解決します。

対数不等式で頻出の問題を5つピックアップして、対数不等式の解き方を解説します。

[st-mybox title=”5つのパターン” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

• 底が1より大きいとき
• 底が1より小さいとき
• 底が異なるとき
• 底が分数のとき
• 底に文字を含むとき

[/st-mybox]

5つの頻出問題を順番に解説していくので、最後までご覧ください。

[st_af id=”13740″]

[st_af id=”13737″]

そもそも対数関数とは？

対数logを含む以下のような関数を対数関数といいます。

[st-mybox title=”対数関数” fontawesome=”fa-check-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\(a>0,a≠1,x>0\)のとき、

\[y=log_{a}x\]

[/st-mybox]

\(a\)は正の数だけれど、1には絶対にならないのもポイントです。

対数関数は、底\(a\)の値によってグラフの形が異なります。

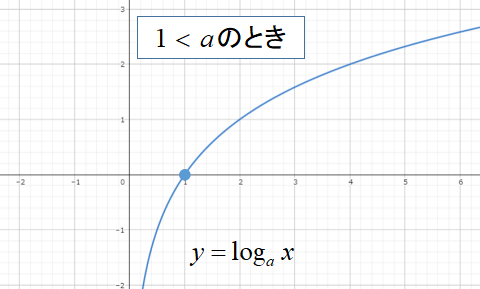
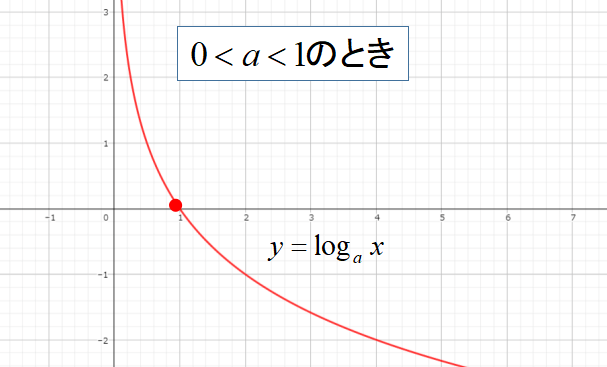
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\(a>1\)のときは、右上がりのグラフ

\(0<a<1\)のときは、右下がりのグラフ

[/st-mybox]

[st-mybox title=”関連記事” fontawesome=”fa-file-text-o” color=”#757575″ bordercolor=”” bgcolor=”#fafafa” borderwidth=”0″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

対数関数のグラフの書き方について解説しました。

⇒対数関数のグラフと書き方3ステップを解説！

[/st-mybox]

対数不等式

対数関数を含む不等式を対数不等式といいます。

[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\[log_{2}x>3\]

\[2log_{3}(2-x)<log_{3}(x+4)\]

[/st-mybox]

この不等式を満たす\(x\)の変域を求めるのが、対数不等式の問題です。

よく出題される5問を用意したので、解き方を確認していきましょう。

また、対数不等式に合わせて、対数方程式も確認しておくとスムーズ理解できます。

>>対数方程式の解き方！真数条件と底の値に注意！

対数不等式を解くときの注意点

対数不等式を解くときは、真数条件と底\(a\)の値に注意しましょう。

真数には「真数は常に正の値である」という条件があります。

[st-mybox title=”真数条件” fontawesome=”fa-exclamation-circle” color=”#ef5350″ bordercolor=”#ef9a9a” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\(y=log_{a}x\)において、真数\(x\)は正の数である。

[/st-mybox]

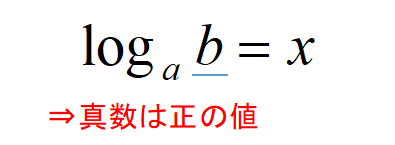
真数条件とあわせて、底\(a\)の値にも注意しましょう。

[st-mybox title=”ポイント” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\(a>0.a≠1,x>0\)において、

\(a>1\)ならば、\(y=log_{a}x\)は増加関数なので

\[log_{a}m<log_{a}n \Leftrightarrow m<n\]

\(0<a<1\)ならば、\(y=log_{a}x\)は減少関数なので

\[log_{a}m<log_{a}n \Leftrightarrow m>n\]

[/st-mybox]

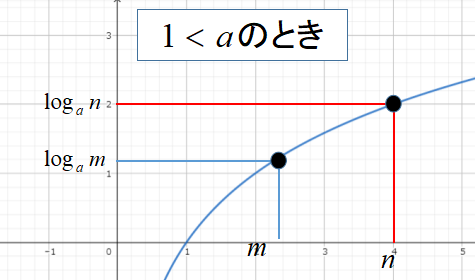
\(a>1\)のときは、グラフが右肩上がりなので

\(log_{a}m<log_{a}n\)のとき、\(m<n\)

が成り立ちます。

[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\(a>1\)のとき、

\[alog_{a}m<log_{a}n \Leftrightarrow m<n\]

[/st-mybox]

しかし、\(0<a<1\)のときはグラフの右肩下がりになるので不等号の向きが逆になります。

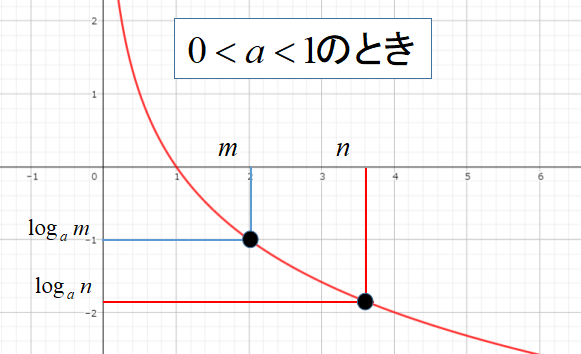
[st-mybox title=”” fontawesome=”” color=”#757575″ bordercolor=”#ccc” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”2″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\(0<a<1\)のとき、

\[log_{a}m<log_{a}n \Leftrightarrow m>n\]

[/st-mybox]

不等式を解いたら、\(a\)の値と不等号の向きをチェックしましょう。

かなり重要なことを言いました。

対数不等式が苦手な方はしっかり読んでください。

対数不等式の解き方を解説！

対数不等式の解き方を解説していきます。

対数不等式では以下の5パターンがよく出題されます。

[st-mybox title=”指数不等式のパターン” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

• 底が1より大きいとき
• 底が1より小さいとき
• 底が異なるとき
• 底が分数のとき
• 底に文字を含むとき

[/st-mybox]

底が1より大きいとき

底が1より大きい対数不等式はシンプルです。

[st-mybox title=”問題①” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

次の対数不等式を解いてみよう。

(1)\(log_{3}x>log_{3}7\)

(2)\(log_{2}x≦3\)

[/st-mybox]

(1)は両辺の底の値が同じなので、このまま真数を比較します。

\[log_{3}x>log_{3}7\]

底3は1より大きいので、不等号の向きは変わりません。

\[x>7\]

(2)は右辺を対数表記にすることで、不等式を解きます。

\begin{eqnarray}
log_{2}x&≦&3\\
log_{2}x&≦&log_{2}8
\end{eqnarray}

底2は1より大きいので、不等号の向きを変えずに比較します。

\[x≦8\]

真数条件から、\(x>0\)なので

\[0<x≦8\]

このパターンは超基本の問題なので、必ず解けるようにしておきましょう。

底が1より小さいとき

底が1より小さい場合は、不等号の向きに注意して下さい。

[st-mybox title=”問題②” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

次の対数不等式を解いてみよう。

(1)\(\displaystyle log_{\frac{1}{2}}x<log_{\frac{1}{2}}3\)

(2)\(\displaystyle log_{\frac{1}{3}}x≧-2\)

[/st-mybox]

(1)は底が1より小さいので、不等号の向きを逆にして真数を比較します。

\begin{eqnarray}
\displaystyle log_{\frac{1}{2}}x&<&log_{\frac{1}{2}}3\\
x&>&3
\end{eqnarray}

不等号の向きによるミスが多発するので、意識して確認しましょう。

問(2)では、両辺を底\(\displaystyle \frac{1}{3}\)の対数にします。

\begin{eqnarray}
\displaystyle log_{\frac{1}{3}}x&≧&-2\\
\displaystyle log_{\frac{1}{3}}x&≧&log_{\frac{1}{3}}\left(\frac{1}{3}\right)^{-2}\\
\displaystyle log_{\frac{1}{3}}x&≧&log_{\frac{1}{3}}9\\
\end{eqnarray}

底が1より小さいので、

\[x≦9\]

真数条件より、\(x>0\)なので

求める不等式の解は

\[0<x≦9\]

底が異なるとき

両辺の底が異なるときは、底の変換公式を用いて底をそろえます。

[st-mybox title=”問題③” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

次の対数不等式を解いてみよう。

\[\displaystyle log_{2}x<log_{4}3\]

[/st-mybox]

まず真数条件より、

\[x>0 \cdots ①\]

与えられた不等式では両辺の底が異なるので、底の変換公式を使いましょう。

[st-mybox title=”底の変換公式” fontawesome=”fa-exclamation-circle” color=”#03A9F4″ bordercolor=”#B3E5FC” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\(a,b,c>0、a,c≠1\)のとき

\[\displaystyle log_{a}b=\frac{log_{c}b}{log_{c}a}\]

[/st-mybox]

両辺の底が2になるように変換します。

\begin{eqnarray}
\displaystyle log_{2}x&<&log_{4}3\\
\displaystyle log_{2}x&<&\frac{log_{2}3}{log_{2}4}\\
\displaystyle log_{2}x&<&\frac{log_{2}3}{2}
\end{eqnarray}

不等式を解いていくと、

\begin{eqnarray}
\displaystyle 2log_{2}x&<&log_{2}3\\
\displaystyle log_{2}x^{2}&<&log_{2}3\\
\end{eqnarray}

底が1より大きいので、

\[x^{2}<3 \cdots ②\]

①,②より、

\[0<x<\sqrt{3}\]

底の変換公式はスムーズに使えるようにしましょう。

底が分数のとき

底が分数だとしても、1との大小関係にさえ注意すれば簡単な問題です。

[st-mybox title=”問題④” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

次の対数不等式を解いてみよう。

(1)\(\displaystyle log_{\frac{7}{10}}x<log_{\frac{7}{10}}3\)

(2)\(\displaystyle log_{\frac{5}{2}}x≦log_{\frac{5}{2}}7\)

[/st-mybox]

(1)は底が1より小さいので、

\[\displaystyle log_{\frac{7}{10}}x<log_{\frac{7}{10}}3\]

不等号の向きに注意して、

\[x>3\]

(2)は底が1より大きいので、不等号の向きは変わりません。

真数条件より、

\[x>0 \cdots ①\]

与えられた不等号を解くと、

\[\displaystyle log_{\frac{5}{2}}x≦log_{\frac{5}{2}}7\]

\[x≦7 \cdots ②\]

①,②より

\[0<x≦7\]

分数があると不安になる気持ちは分かりますが、難しい問題ではないので冷静に対処しましょう。

底に文字を含むとき

底に文字を含むときは、場合分けをして考えます。

[st-mybox title=”問題②” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

次の対数不等式を解いてみよう。

\[log_{a}x<log_{a}5\]

[/st-mybox]

底\(a\)の値によって、不等号の向きが変わるので場合分けして考えましょう。

まず真数条件より

\[x>0 \cdots ①\]

底の条件から\(a>0,a≠1\)なので、以下の2つに場合分けして考えます。

[st-mybox title=”” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

(ⅰ)\(a>1\)のとき
(ⅱ)\(0<a<1\)のとき

[/st-mybox]

(ⅰ)\(a>1\)のとき

\[log_{a}x<log_{a}5\]

\[x<5\]

①より、

\[0<x<5\]

(ⅱ)\(0<a<1\)のとき

\[log_{a}x<log_{a}5\]

\[x>5\]

したがって、不等式を解くと

\begin{eqnarray}
0<x<5&（&a>1のとき）\\
x>5&（&0<a<1のとき）
\end{eqnarray}

このように、底や真数に文字が含まれているときは、自分で場合分けをして不等式を解きましょう。

[st-wide-background myclass=”” backgroud_image=”” bgcolor=”#fafafa” align=”” add_style=”margin-bottom:0px; border-top:2px #ccc solid; border-bottom:2px #ccc solid;”]

基礎から丁寧に確認！
プロ講師の分かりやすい解説

[/st-wide-background]

[st-wide-background myclass=”” backgroud_image=”” bgcolor=”#ffffff” align=”” add_style=””]

ここまで読んで、まだピンと来ていない人いますか？

もしかすると、あなたには文章よりも動画解説のほうが合っているかもしれません。

河合塾が提供する「河合塾One」なら解説が丁寧で、基礎から確認できるのでおすすめです。

しかも、いまなら無料体験で全授業が視聴できます。

[/st-wide-background]

対数不等式【練習問題】

[st-wide-background myclass=”” backgroud_image=”” bgcolor=”#fafafa” align=”” add_style=”margin-top:0px; margin-bottom:0px;”]

対数不等式の練習問題に挑戦してみましょう。

以下が今回の練習問題です。

[st-mybox title=”練習問題” fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

次の不等式を解いてみよう。

(1)\(\displaystyle log_{\frac{1}{3}}(3-2x)≦log_{\frac{1}{3}}x\)

(2)\(log_{3}x≦log_{9}5\)

(3)\(\displaystyle log_{a}(x-3)≦log_{a}5\)

[/st-mybox]

[/st-wide-background]

練習問題1の解説

[st-mybox title=”練習問題1″ fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

次の不等式を解いてみよう。

(1)\(\displaystyle log_{\frac{1}{3}}(3-2x)≦log_{\frac{1}{3}}x\)

[/st-mybox]

これは底が1より小さい対数不等式の問題ですね。

真数は正であるので、\(3-2x>0\)かつ\(x>0\)

すなわち、\(\displaystyle 0<x<\frac{3}{2} \cdots ①\)

底\(\displaystyle \frac{1}{3}\)は1より小さいので

\begin{eqnarray}
\displaystyle log_{\frac{1}{3}}(3-2x)&≦&log_{\frac{1}{3}}x\\
3-2x&≧&x\\
1&≧&x　\cdots ②
\end{eqnarray}

①,②より、

\[0<x≦1\]

練習問題2の解説

[st-mybox title=”練習問題2″ fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

次の不等式を解いてみよう。

(2)\(log_{3}x≦log_{9}5\)

[/st-mybox]

まずは両辺の底をそろえましょう。

\begin{eqnarray}
\displaystyle log_{3}x&≦&\frac{log_{3}5}{log_{3}9}\\
\displaystyle log_{3}x&≦&\frac{log_{3}5}{2}
\end{eqnarray}

両辺の底を合わせることができたので、不等式を解いていきます。

\begin{eqnarray}
\displaystyle 2log_{3}x&≦&log_{3}5\\
\displaystyle log_{3}x^{2}&≦&log_{3}5
\end{eqnarray}

底3は1より大きいので、

\begin{eqnarray}
x^{2}&≦&5\\
-\sqrt{5}≦&x&≦\sqrt{5}　\cdots ①
\end{eqnarray}

真数は正なので、\(x>0 \cdots ②\)

①,②より、

\[0<x≦\sqrt{5}\]

練習問題3の解説

[st-mybox title=”練習問題3″ fontawesome=”fa-check-circle” color=”#757575″ bordercolor=”#BDBDBD” bgcolor=”#ffffff” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

次の不等式を解いてみよう。

(3)\(\displaystyle log_{a}(x-3)≦log_{a}5\)

[/st-mybox]

底に文字を含んでいるので、場合分けが必要です。

真数は正なので、\(x>3 \cdots ①\)

底の条件より、\(a>0,a≠1\)

(ⅰ)a>1のとき

\begin{eqnarray}
\displaystyle log_{a}(x-3)&≦&log_{a}5\\
x-3&≦&5\\
x&≦&8　\cdots ②
\end{eqnarray}

①,②より、

\[0<x≦8\]

(ⅱ)0<a<1のとき

\begin{eqnarray}
\displaystyle log_{a}(x-3)&≦&log_{a}5\\
x-3&≧&5\\
x&≧&8
\end{eqnarray}

したがって、

\begin{eqnarray}
0<&x&≦8（a>1のとき）\\
x&≧&8（0<a<1のとき）
\end{eqnarray}

対数不等式の解き方　まとめ

今回は対数不等式についてまとめました。

[st-marumozi fontawesome=”” bgcolor=”#FFB74D” bordercolor=”” color=”#fff” radius=”30″ margin=”0 10px 10px 0″ myclass=””]対数不等式　まとめ[/st-marumozi]

対数不等式は以下の2つに注意すること。

[st-mybox title=”ポイント” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”#FFFDE7″ borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

• 真数条件
• 底が1より大きいか小さいか

[/st-mybox]

底の値によって不等号の向きに注意しましょう。

[st-mybox title=”注意ポイント” fontawesome=”fa-exclamation-circle” color=”#ef5350″ bordercolor=”#ef9a9a” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

\(a>0.a≠1,x>0\)において、

\(a>1\)ならば、\(y=log_{a}x\)は増加関数なので

\[log_{a}m<log_{a}n \Leftrightarrow m<n\]

\(0<a<1\)ならば、\(y=log_{a}x\)は減少関数なので

\[log_{a}m<log_{a}n \Leftrightarrow m>n\]

[/st-mybox]

以下の5パターンはよく出題されるので、解き方に慣れておきましょう。

[st-mybox title=”指数不等式のパターン” fontawesome=”fa-check-circle” color=”#FFD54F” bordercolor=”#FFD54F” bgcolor=”” borderwidth=”2″ borderradius=”5″ titleweight=”bold” fontsize=”” myclass=”st-mybox-class” margin=”25px 0 25px 0″]

• 底が1より大きいとき
• 底が1より小さいとき
• 底が異なるとき
• 底が分数のとき
• 底に文字を含むとき

[/st-mybox]

今回は対数不等式について解説しました。

底の変換公式や対数法則を使った計算もあるので、対数logが不安な方は以下の記事もご覧ください。

>>底の変換公式を解説！証明と底を決めるコツが分かる！

定期テストに向けて指数・対数の復習をするならこちらの記事がおすすめです。

>>指数関数・対数関数logの公式や性質を徹底解説！

[st-mybutton class=”” url=”https://math-travel.jp/shisuu-log/” title=”指数関数・対数関数のまとめ記事へ” rel=”” fontawesome=”” target=”” color=”#9CCC65″ bgcolor=”” bgcolor_top=”” bordercolor=”#9CCC65″ borderwidth=”3″ borderradius=”30″ fontsize=”” fontweight=”bold” width=”” fontawesome_after=”fa-chevron-right” shadow=”” ref=”” beacon=””]