二次関数の軸・頂点の求め方を解説！平方完成ができればOK！

数学Ⅰ二次関数には「軸と頂点を求める問題」が多くあります。

本記事では、2次関数の頂点や軸の求め方を解説します。

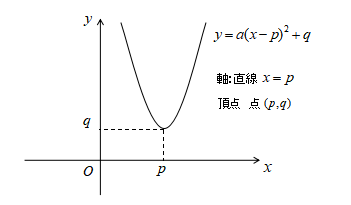
2次関数の軸や頂点は以下の形で求めることができます。

2次関数の軸と頂点

2次関数の軸や頂点を求めるには、式を以下の形にすることで求められます。

この2次関数は$y=ax^{2}$のグラフをx軸方向に$p$、y軸方向に$q$だけ平行移動した2次関数を表しています。

頂点と軸の求め方

2次関数の頂点と軸の求め方は主に2つあります。

平方完成で求める方法

まずは平方完成を用いて軸と頂点を求める方法から解説します。

平方完成とは以下のような式変形です。

$$\begin{eqnarray} x^{2}+4x&=&(x^{2}+4x+4)-4\ &=&(x+2)^{2}-4 \end{eqnarray}$$

$$\begin{eqnarray} x^{2}-6x+4&=&(x^{2}-6x+9)-9+4\ &=&(x-3)^{2}-5 \end{eqnarray}$$

2次関数$x^{2}+6x+5$のグラフの軸と頂点を求めます。

$$\begin{eqnarray} x^{2}+6x+5&=&(x^{2}+6x+9)-9+5\\ &=&(x+3)^{2}-4 \end{eqnarray}$$

ここで以下のことを思い出してください。

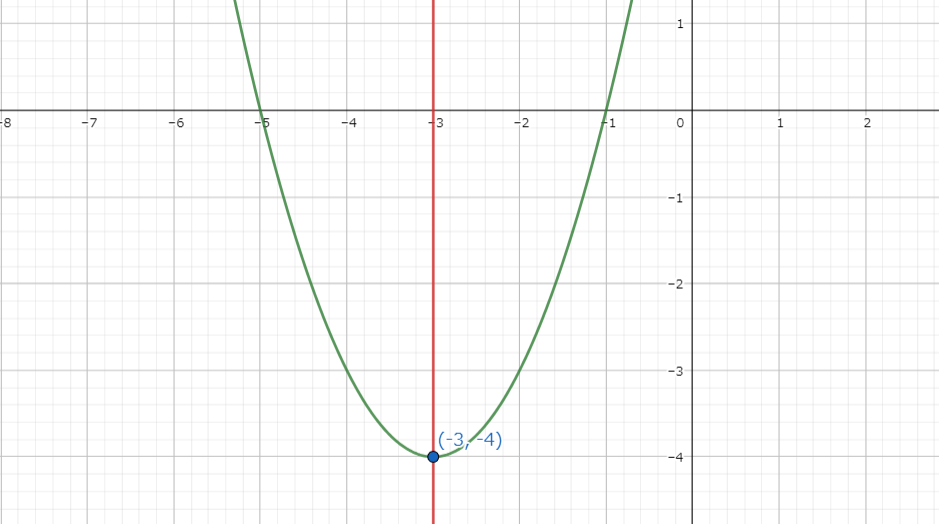
$(x+3)^{2}-4$のグラフの軸と頂点は、

放物線の軸：$x=-3$
頂点の座標：$(-3,-4)$

だと分かります。

これで$y=x^{2}+6x+5$の軸と頂点の座標を求めることができました。

このように、平方完成をして$y=a(x-p)^{2}+q$の形にできれば、軸も頂点が分かります。

公式を暗記して求める方法

２次関数の軸と頂点を求めるもう1つの方法として、公式に代入する方法があります。

ただしこのやり方は、以下の公式を覚える必要があるのであまりオススメはしません。

2次関数$x^{2}+6x+5$のときの軸は

$$\begin{eqnarray} x&=&-\frac{b}{2a}\\ &=&-\frac{6}{2 \cdot 1}\\ &=&-3 \end{eqnarray}$$

したがって、放物線の軸は$x=-3$

 

また、2次関数$x^{2}+6x+5$の頂点は

$$\begin{eqnarray} 頂点のy座標&=&-\frac{b^{2}-4ac}{4a}\\ &=&-\frac{6^{2}-4 \cdot 1 \cdot 5}{4 \cdot 1}\\ &=&-4 \end{eqnarray}$$

したがって、2次関数$x^{2}+6x+5$の頂点は$(-3,-4)$となります。

平方完成ができれば2次関数のグラフを書くことができます。

グラフの書き方は「2次関数のグラフの書き方を3ステップで解説！」にて詳しく解説しました。

分数やマイナスをもつ2次関数の頂点

以下の2つの式のように、頂点を求めたい2次関数が分数・マイナスを含む場合もあります。

$$\displaystyle y=x^{2}+\frac{6}{5}x+3 \cdots ①$$

$$y=-x^{2}+6x+3 \cdots ②$$

難しそうに見えますが、落ち着いて対処すれば問題ないです。

分数を含む2次関数

2次関数$\displaystyle x^{2}+\frac{6}{5}x+3$の軸と頂点を考えましょう。

やはり気になるのは、$\displaystyle \frac{6}{5}x$ですよね。

 今回は平方完成を用いた求め方をします。

$$\begin{eqnarray} y&=&x^{2}+\frac{6}{5}x+3\\ &=&(x^{2}+\frac{6}{5}x+\frac{9}{25})-\frac{9}{25}+3\\ &=&(x+\frac{3}{5})^{2}+\frac{66}{25}\\ \end{eqnarray}$$

したがって、分数を含む2次関数の軸・頂点も求めることができました。

放物線の軸：$\displaystyle x=-\frac{3}{5}$
頂点の座標：$\displaystyle (-\frac{3}{5},\frac{66}{25})$

マイナスを含む2次関数

次にマイナスを含む2次関数もみていきましょう。

$-x^{2}+6x+3$の軸と頂点の座標を求めます。

$$\begin{eqnarray} y&=&-x^{2}+6x+3\\ &=&-(x^{2}-6x)+3\\ &=&-{(x^{2}-6x+9)-9}+3\\ &=&-(x-3)^{2}+12\\ \end{eqnarray}$$

したがって、

放物線の軸：$x=3$
頂点の座標：$\displaystyle (3,12)$

頂点と軸の求め方《おすすめ動画》

ここまで軸と頂点の求め方を解説してきました。

「イマイチ分からないなぁ…」

そんな方は下の動画がおすすめです。

▽2次関数の軸と頂点の説明をしています

頂点と軸の求め方《練習問題》

それでは、2次関数の軸と頂点を求める練習をしましょう。

以下の2次関数の軸と頂点を求めます。

$y=x^{2}+2x+4$の軸と頂点

2次関数$y=x^{2}+2x+4$を平方完成します。

$$\begin{eqnarray} y&=&x^{2}+2x+4\\ &=&(x^{2}+2x+1)-1+4\\ &=&(x+1)^{2}+3 \end{eqnarray}$$

したがって、

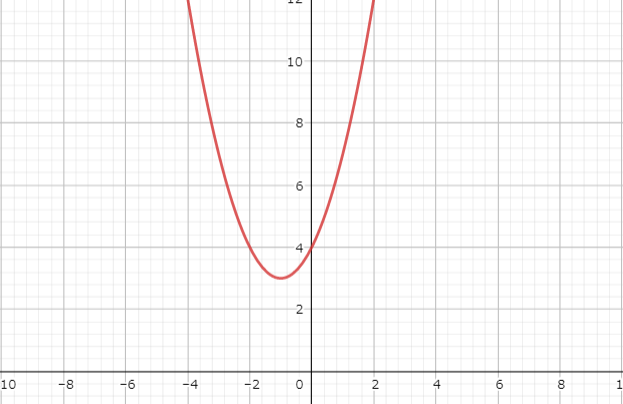
解答
放物線の軸：$x=-1$
頂点の座標：$(-1,3)$

$y=3x^{2}+6x-4$の軸と頂点

2次関数$y=3x^{2}+6x-4$を平方完成します。

$$\begin{eqnarray} y&=&3x^{2}+6x-4\\ &=&3(x^{2}+2x)-4\\ &=&3\{(x^{2}+2x+1)-1\}-4\\ &=&3(x^{2}+1)^{2}-7 \end{eqnarray}$$

したがって、

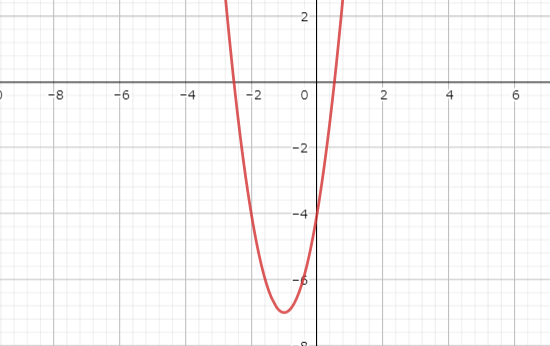
解答
放物線の軸：$x=-1$
頂点の座標：$(-1,-7)$

$y=-2x^{2}-4x+5$の軸と頂点

2次関数$y=-2x^{2}-4x+5$を平方完成します。

$$\begin{eqnarray} y&=&-2x^{2}-4x+5\\ &=&-2(x^{2}+2x)+5\\ &=&-2\{(x^{2}+2x+1)-1\}+5\\ &=&-2(x^{2}+1)^{2}+7 \end{eqnarray}$$

したがって、

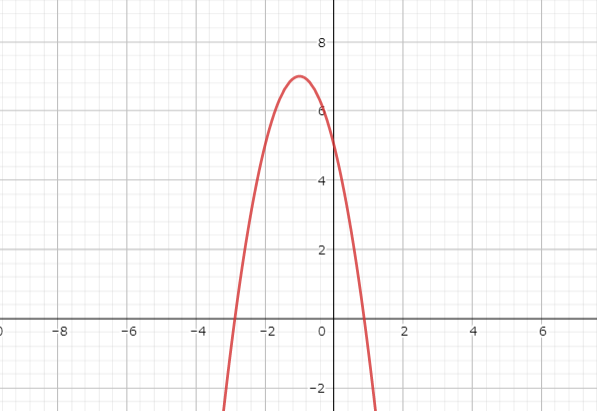
解答
放物線の軸：(x=-1)
頂点の座標：((-1,7))

2次関数のおすすめ勉強法

2次関数は高校数学のなかでも解きやすい問題が多い単元です。

問題の意図をしっかり理解できれば、解法もすぐに思いつけるようになります。

次は2次関数のおすすめ勉強法を紹介します。

自分のいまの理解度と目標を照らし合わせて、自分に合った勉強法を試してみてください。

教科書やノートを見直す

まずは基本に立ち返って、教科書・ノートを見直してみましょう。

教科書には重要なポイントがギュッと詰まっています。

2次関数の基本は「2次関数の公式まとめ」にて解説しているのでご覧ください。

問題集で応用力を磨く

2次関数の関する公式に慣れてきたら、次は問題を解いて応用力を磨きましょう。

問題の難易度をステップアップさせていくと、自分がどこで分からなくなったか把握しやすいです。

分かりやすい解説を見る

以下のような悩みがあるなら映像授業もおすすめです。

映像授業なら必要な授業のみを選び、分かるまで何度も視聴することができます。

分からないを1つずつ解消できるので、定期テストで高得点を取りたい方に授業授業がおすすめです。

2次関数の頂点・軸　まとめ

今回は2次関数の軸と頂点の求め方についてまとめました。

2次関数の頂点や軸が求められるとグラフが書けるようになります。

また、スムーズにグラフが書けることで2次関数の最大値・最小値の問題も解きやすくなります。

平方完成が苦手という方も多いと思いますが、軸や頂点の座標は求められるようにしたいので一緒に頑張りましょう。

それでは最後までご覧いただきありがとうございました。

みんなの努力が報われますように！